In a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

Step by step video, text & image solution for In a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=1/2(AB-CD). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (long Answer Questions)
5 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise
10 Videos
Similar Questions
Knowledge Check
ABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :
 A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2
A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2In trapezium ABCD,AB∣∣CDwith AB=24cm.andCD=16cm. P and Q are mid-points of the diagonals AC and BD respectively. Find the length of PQ.
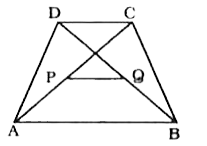 A4 cmB5 cmC8 cmD6 cm
A4 cmB5 cmC8 cmD6 cm
In the given figure ABCD is a trapezium with AB || DC. E and F are respectively midpoint of AD and BC. Prove that, EF=12(AB+CD)
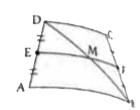
View SolutionIf ABCD is quadrilateral and EandF are the mid-points of ACandBD respectively, prove that →AB+→AD +→CB +→CD =4 →EF.
View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE triset (divide into three equal parts) the diagonal BD.

View SolutionIf M and N are the mid-points of the diagonals AC and BD respectively of a quadrilateral ABCD, then the of −−→AB+−−→AD+−−→CB+−−→CD equals
View SolutionIn a trapezium ABCD, P and Q are points on AD and Bc respectively such that DPAP=CQBQ=13.If the diagonal BD intersects PQ at E,find the ratio of arΔDPE toarea of trapezium ABCD.
View SolutionABCD is a rectangle and E F G and H are the mid-points of AB BC CD DA respectively Prove that EFGH is a rhombus
View Solution


