In a triangle ABC, D and E are points on AB, AC respectively such that DE is parallel to BC. Suppose BE, CD intersect at O. If the areas of the triangles ADE and ODE are 3 and 1 respectively, find the area of the triangle ABC, with justification

Video Solution

Text Solution

Verified by Experts

We denote the area of triangle PQR by [PQR]. We see that [BOD] and [COE] are equal. Let the common value be x, and let [BOC] = t. Using the fact that the ratio of areas of two triangles having equal altitudes is the same as the ratio of their respective bases, we obtain.
$\frac{x}{1} = \frac{B O}{O E} = \frac{t}{x}$ .

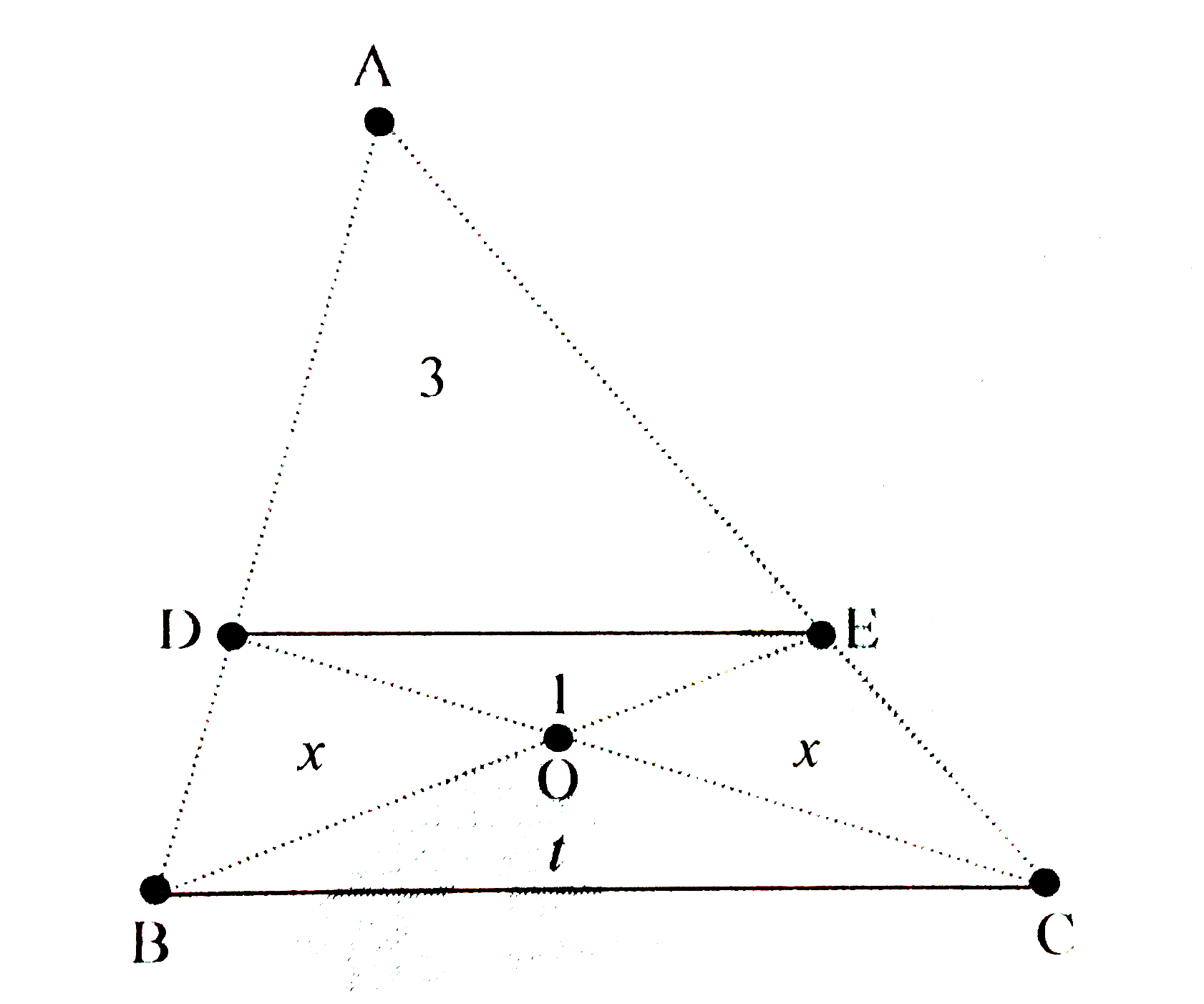
This gives $t = x^{2}$ . Now ADE and ABC are similar so that
$\frac{[A D E]}{[A B C]} = \frac{D E^{2}}{B C^{2}} = \frac{[O D E]}{[O B C]}$ ,
since ODE and OCB are also similar. This implies that
$\frac{3}{4 + 2 x + t} = \frac{1}{t}$ ,
which simplifies to t=2+x, using $t = x^{2}$ we get a quadratic in $x : x^{2} - x - 2 = 0$ . Its solution are x=2 and x=-1. Since x cannot be negative, x=2 and t=4. Thus $[A B C] = 4 + 2 x + t = 4 + 4 + 4 = 12$

Updated on:21/07/2023

Area of $Δ A B C = 30 c m^{2}$ . D and E are the mid - points of BC and AB respectively. Find $A (Δ B D E)$ :
A $10 c m^{2}$
B $7.5 c m^{2}$
C $15 c m^{2}$
Dnone of these
$Δ A B C$ is an equilateral triangle and D and E are midpoints of AB and BC respectively. Then the area of $Δ A B C$ : the area of the trapezium ADEC is
A $5 : 3$
B $4 : 1$
C $8 : 5$
D $4 : 3$
In a triangle ABC, points P, Q and R are the mid-points of the sides AB, BC and CA respectively. If the area of the triangle ABC is 20 sq. units, find the area of the triangle PQR
A10 sq. units
B5.3 sq. units
C5 sq. units
DNone of these