In a triangle ABC $I_{1}, I_{2}, I_{3}$ are excentre of triangle then show that $I I_{1} . I I_{2} . I I_{3} = 16 R^{2} r .$ Solution in Punjabi

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $I I_{1} . I I_{2} . I I_{3} = 64 R^{3} . \frac{r}{4 R} = 16 R^{2} r$

Updated on:21/07/2023

Answer

Step by step video & image solution for In a triangle ABC I_1, I_2,I_3 are excentre of triangle then show that II_(1). II_(2). II_(3)=16R^(2)r. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS PROPERTIES AND SOLUTION OF TRIANGLES

Topper's Solved these Questions

PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - SOLVED EXAMPLES
1 Videos
PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 1
20 Videos
PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
52 Videos
SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos

Similar Questions

Match the statements of Column I with values of Column II.

View Solution
In the given figure,if $A B = A C, ∠ B A D = 30^{\circ} and A E = A D,$ then x is equal to

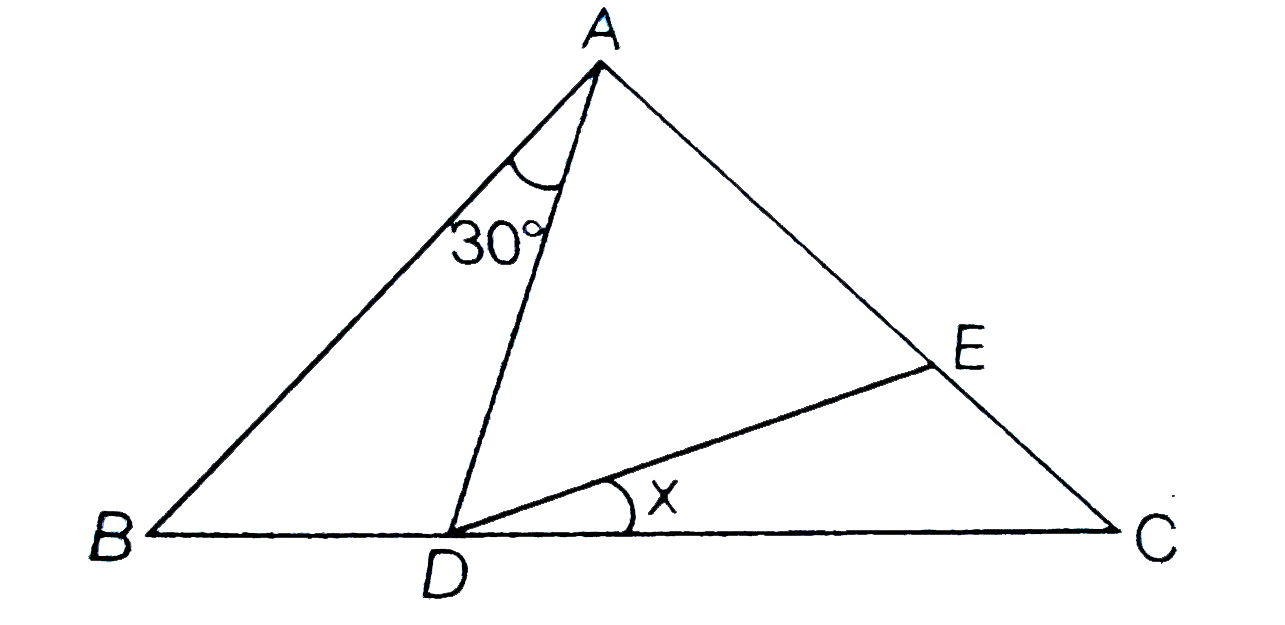
View Solution
Let O be the origin and let PQR be an arbitrary triangle. The point S is such that $¯ ¯¯¯¯ ¯ O P \cdot ¯ ¯¯¯¯ ¯ O Q + ¯ ¯¯¯¯ ¯ O R \cdot ¯ ¯¯¯¯ ¯ O S = ¯ ¯¯¯¯ ¯ O R \cdot ¯ ¯¯¯¯ ¯ O P + ¯ ¯¯¯¯ ¯ O Q \cdot ¯ ¯¯¯¯ ¯ O S = ¯ ¯¯¯¯ ¯ O Q \cdot ¯ ¯¯¯¯ ¯ O R + ¯ ¯¯¯¯ ¯ O P \cdot ¯ ¯¯¯¯ ¯ O S$ Then the triangle PQR has S as its
View Solution
Let a,b,c be in A.P. and $| a | < 1, | b | < 1 | c | < 1 . if x = 1 + a + a^{2} + . . . . to \infty, y = 1 + b + b^{2} + . . . . to \infty and, z = 1 + c + c^{2} + . . . to \infty$ , then x,y,z are in
View Solution
If in triangle $A B C, \sum \frac{sin A}{2} = \frac{6}{5} a n d \sum I I_{1} = 9$ (where $I_{1}, I_{2} a n d I_{3}$ are excenters and $I$ is incenter, then circumradius $R$ is equal to $\frac{15}{8}$ (b) $\frac{15}{4}$ (c) $\frac{15}{2}$ (d) $\frac{4}{12}$
View Solution
If is the incentre of $Δ A B C and I_{1}$ , is the excentre opposite to the vertex. 'A' of $Δ A B C$ , thern $I I_{1} =$
View Solution
If I_(1),I_(2),I_(3) and I are the excenter and incentres of Delta ABC respectively,then (II_(1))).(II_(2))*(II_(3))=
View Solution
Statement I If I is incentre of $Δ A B C and I_{1}$ excentre opposite to A and P is intersection of $I I_{1}$ and BC, then $I P . I_{1} P = B p . P C$
Statement II In a $Δ A B C,$ I is incentre and $I_{2}$ is excentre opposite to A, then IBI, $I_{1},$ C must be square.
View Solution
In a $Δ A B C$ , if ${(I I_{1})}_{1}^{2} + {(I_{2} I_{3})}_{2}^{2} = λ R^{2}$ , where I denotes incentre, $I_{1}, I_{2} and I_{3}$ denote centres of the circles escribed to the sides BC, CA and AB respectively and R be the radius of the circum circle of $Δ A B C$ . Find $λ$ .
View Solution
If 1 is the incentre and $I_{1}, I_{2}, I_{3}$ are the centre of escribed circles of the $△ A B C$ . Prove that
$I I_{1}^{2} + I_{2} I_{3}^{2} = I I_{2}^{2} + I_{3} I_{1}^{2} = I_{1} I_{2}^{2} + I I_{3}^{2}$
View Solution
If I is the incentre of a triangle whose is radius and circumradius are r and R respepectively : $I_{1}, I_{2}, I_{3}$ is its ex-centre triangle, then $I I_{1} . I I_{2} . I I_{3}$ is equal to
View Solution
If $I_{r}^{2} + m_{r}^{2} + n_{r}^{2} = 1$ where r=1,2,3 and $I_{1} I_{2} + m_{1} m_{2} + n_{1} n_{2} = 0$ …..etc. then
$Δ = {∣ ∣ ∣ ∣ \begin{matrix} I_{1} & m_{1} & n_{1} I_{2} & m_{2} & n_{2} I_{3} & m_{3} & n_{3} \end{matrix} ∣ ∣ ∣ ∣}^{2}$ is equal to
View Solution
In a $Δ A B C$ , if ${(I I_{1})}_{1}^{2} + {(I_{2} I_{3})}_{2}^{2} = λ R^{2}$ , where I denotes incentre, $I_{1}, I_{2} and I_{3}$ denote centres of the circles escribed to the sides BC, CA and AB respectively and R be the radius of the circum circle of $Δ A B C$ . Find $λ$ .
View Solution
$I, I_{1}, I_{2}, I_{3}$ are the in centre and excentres of $Δ A B C$ .If $I (0, 0), I_{1} (2, 3), I_{2} (5, 7)$ then the, distance between the orthocentres of $Δ I I_{1} I_{3}$ and $Δ I_{1} I_{2} I_{3} i s$
View Solution
If $I_{1}, I_{2}, I_{3}$ are the centers of escribed circles of triangle $A B C,$ show that area of triangle $I_{1} I_{2} I_{3} = \frac{a b c}{2 r} .$
View Solution
$I_{1} = \int_{0}^{\frac{π}{2}} \frac{sin x - cos x}{1 + sin x cos x} d x, I_{2} = \int_{0}^{2 π} {cos}^{6} x d x, I_{3} = \int_{\frac{π}{2}}^{\frac{π}{2}} {sin}^{3} x d x, I_{4} = \int_{0}^{1} 1 n (\frac{1}{x} - 1) d x . T h e n$ $I_{2} = I_{3} = I_{4} = 0, I_{1} \neq 0$ $I_{1} = I_{2} = I_{3} = 0, I_{4} \neq 0$ $I_{1} = I_{2} = I_{3} = 0, I_{4} \neq 0$ $I_{1} = I_{4} = I_{3} = 0, I_{2} \neq 0$
View Solution

ARIHANT MATHS-PROPERTIES AND SOLUTION OF TRIANGLES -Exercise (Questions Asked In Previous 13 Years Exam)

In a triangle ABC I1, I2,I3 are excentre of triangle then show that ...
02:34
Prove that 2sin^2(pi/6) - sec^2(pi/3)= -7/2
02:03
In a triangle the sum of two sides is x and the product of the same is...
05:17
Consider a triangle A B C and let a , b and c denote the lengths of th...
03:54
Solution of differential equation 2xy dy / dx = x^2 + 3y^2 is .
02:52
Let PQR be a triangle of area Delta with a = 2, b = 7//2, and c = 5//2...
04:13
If the angle A ,Ba n dC of a triangle are in an arithmetic propression...
03:49
Let A B C be a triangle such that /A C B=pi/6 and let a , b and c deno...
05:06
A triangle A B C with fixed base B C , the vertex A moves such that co...
04:32
Let A B Ca n dA B C ' be two non-congruent triangles with sides A B=4,...
04:26
A straight line through the vertex P of a triangle P Q R intersects th...
06:17
Consider the circle x^2 + y^2 = 9 and the parabola y^2 = 8x. They inte...
08:21
Consider the circle x^2 + y^2 = 9 and the parabola y^2 = 8x. They inte...
08:21
Consider the circle x^2 + y^2 = 9 and the parabola y^2 = 8x. They inte...
08:21
Internal bisector of /A of triangle ABC meets side BC at D. A line dra...
04:41
One angle of an isosceles triangle is 120^0 and the radius of its incr...
05:49
In Delta ABC, which one is true among the following ?
01:40
Let a vertical tower A B have its end A on the level ground. Let C be ...
02:45
ABCD is a trapezium such that AB and CD are parallel and BC bot CD. If...
04:13
For a regular polygon, let r and R be the radii of the inscribed and t...
03:37
In triangle A B C , let /c=pi/2dot If r is the inradius and R is circu...
02:21

Home
Ask Doubt
Profile

In a triangle ABC I 1 , I 2 , I 3 are excentre of triangle then show that I I 1 . I I 2 . I I 3 = 16 R 2 r . Solution in Punjabi

The correct Answer is: I I 1 . I I 2 . I I 3 = 64 R 3 . r 4 R = 16 R 2 r

Topper's Solved these Questions

Similar Questions

ARIHANT MATHS-PROPERTIES AND SOLUTION OF TRIANGLES -Exercise (Questions Asked In Previous 13 Years Exam)

In a triangle ABC $I_{1}, I_{2}, I_{3}$ are excentre of triangle then show that $I I_{1} . I I_{2} . I I_{3} = 16 R^{2} r .$ Solution in Punjabi

The correct Answer is: $I I_{1} . I I_{2} . I I_{3} = 64 R^{3} . \frac{r}{4 R} = 16 R^{2} r$