In a triangle ABC with ∠A=90∘, P is a point on BC such that PA : PB = 3 : 4 If AB=√7 and AC=√5 then BP : PC is-
2:1
:3
4:5
8:7
The correct Answer is:A
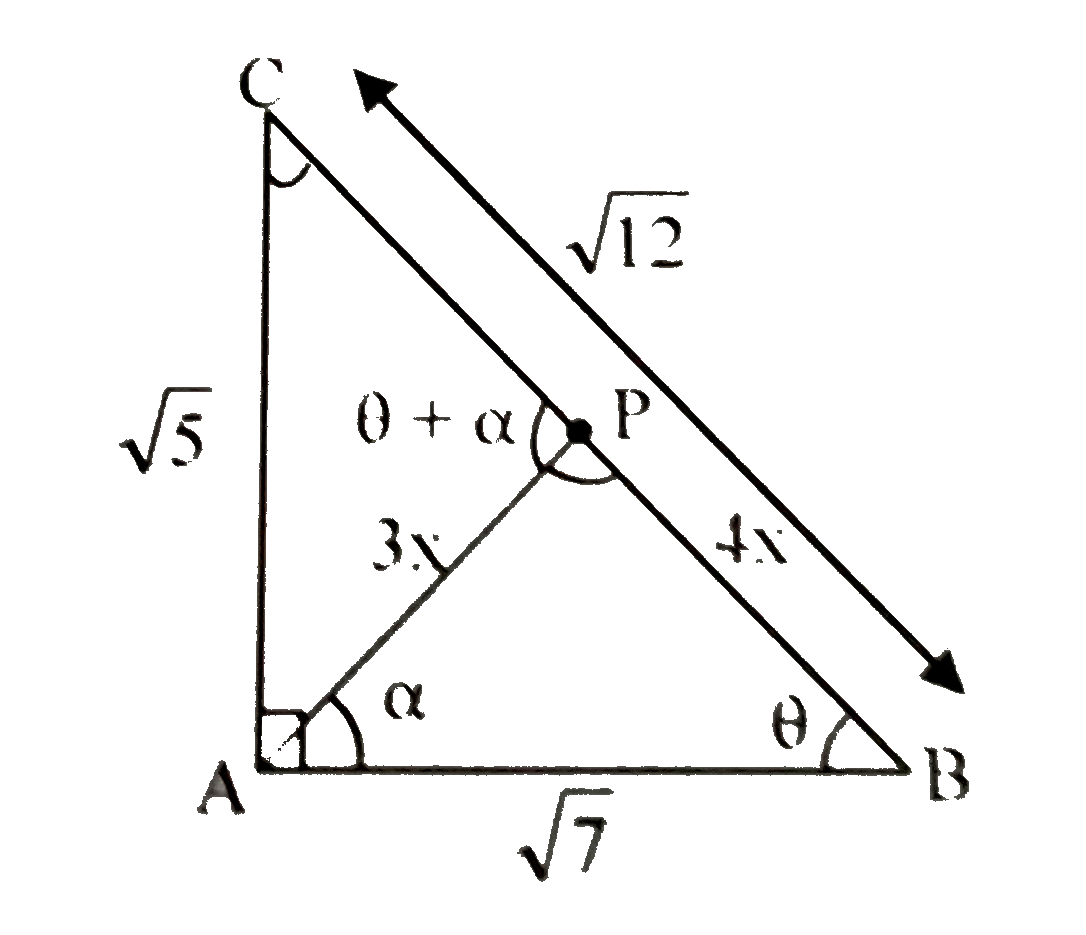
tanθ=√5√7,sinθ=√5√12,cosθ=√7√12
In ΔAPB using sine rule
3Xsinθ=4Xsinα=√7sin(180∘−(θ+α))
sinα=43sinθ=43×√5√12=2√53√5=√20√27
⇒cosα=√7√27
&3xsin(θ+α)=√7sinθ
⇒3x(cosα+cotθsinα)=√7
⇒3x(√3√27)+√7√5√20√27)=√7
3x×1√3=1
x=1√3
∴BPPC=4x√12−4x=12√34/√3−1=46−4=21
Topper's Solved these Questions
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Matematics
20 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part 1 Mathematics
45 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-2 MATHMATICS
10 Videos
- KVPY 2021BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART II MATHEMATICS
4 Videos
Similar Questions
In any triangle ABC, if∠C=90∘, AC=4 unit, BC=3, find AB.
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 3 : 4 and Q is the midpoint of BP. Then ar(△ABQ):ar(△ABC) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 3 : 4 है और Q, BP का मध्य बिंदु है | ar(△ABQ):ar(△ABC) का मान ज्ञात करें |
View Solution
Knowledge Check
In right △ABC, AB=BC , then ∠A is equal to
A45∘B90∘C60∘DNone of theseIn ΔABC,∠B=90∘. If P is the mid-point of side AC, then
PA=PB=AACB3ACC12ACD2AC
In △ABC ,P is a point on BC such that BP : PC = 2 : 3 and Q is the midpoint of BP. Then (△ABQ):(△ABC) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 2 : 3 है और Q, BP का मध्य बिंदु है | (△ABQ):(△ABC) ज्ञात करें |
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 4:5 and Q is the midpoint of BP. Then ar(△ABQ):ar(△ABC) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 4:5 है और Q, BP का मध्य बिंदु है | ar(△ABQ):ar(△ABC) का मान ज्ञात करें |
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 4 : 11 and Q is the midpoint of BP. Then ar(△ABQ):ar(△ABC) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 4 : 11 है और Q, BP का मध्य बिंदु है | ar(△ABQ):ar(△ABC) का मान किसके बराबर होगा ?
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 4 : 3 and Q is the midpoint of BP. Then ar(△ABQ):ar(△ACB) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 4 : 3 है और Q, BP का मध्य बिंदु है | ar(△ABQ):ar(△ACB) का मान ज्ञात करें |
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 1 : 2 and Q is the mid point of BP. then, ar(△ABQ):ar(△ABC) is equal to:
त्रिभुज ABC में, P, BC पर स्थित ऐसा बिंदु है कि BP : PC = 1 : 2 है और Q, BP का मध्य बिंदु है | तो ar(△ABQ):ar(△ABC) का मान क्या होगा ?
View SolutionIn a triangle ABC, ∠C=60∘and∠A=75∘ If D is a point on AC such that the area of the ΔBAD is √3 times the area of the ΔBCD, then the ∠ABD is
View Solution
