In an equilateral triangle ABC, D is a point on side BC such that $B D = \frac{1}{3} B C$ . Prove that $9 A D^{2} = 7 A B^{2}$ .

Video Solution

Text Solution

Verified by Experts

GIVEN $A Δ A B C$ in which $A B = B C = C A$ and D is a point on BC such that $B D = \frac{1}{3} B C$ .
TO PROOVE $9 A D^{2} = 7 A B^{2}$
CONSTRUCTION Draw $A L ⊥ B C$ .

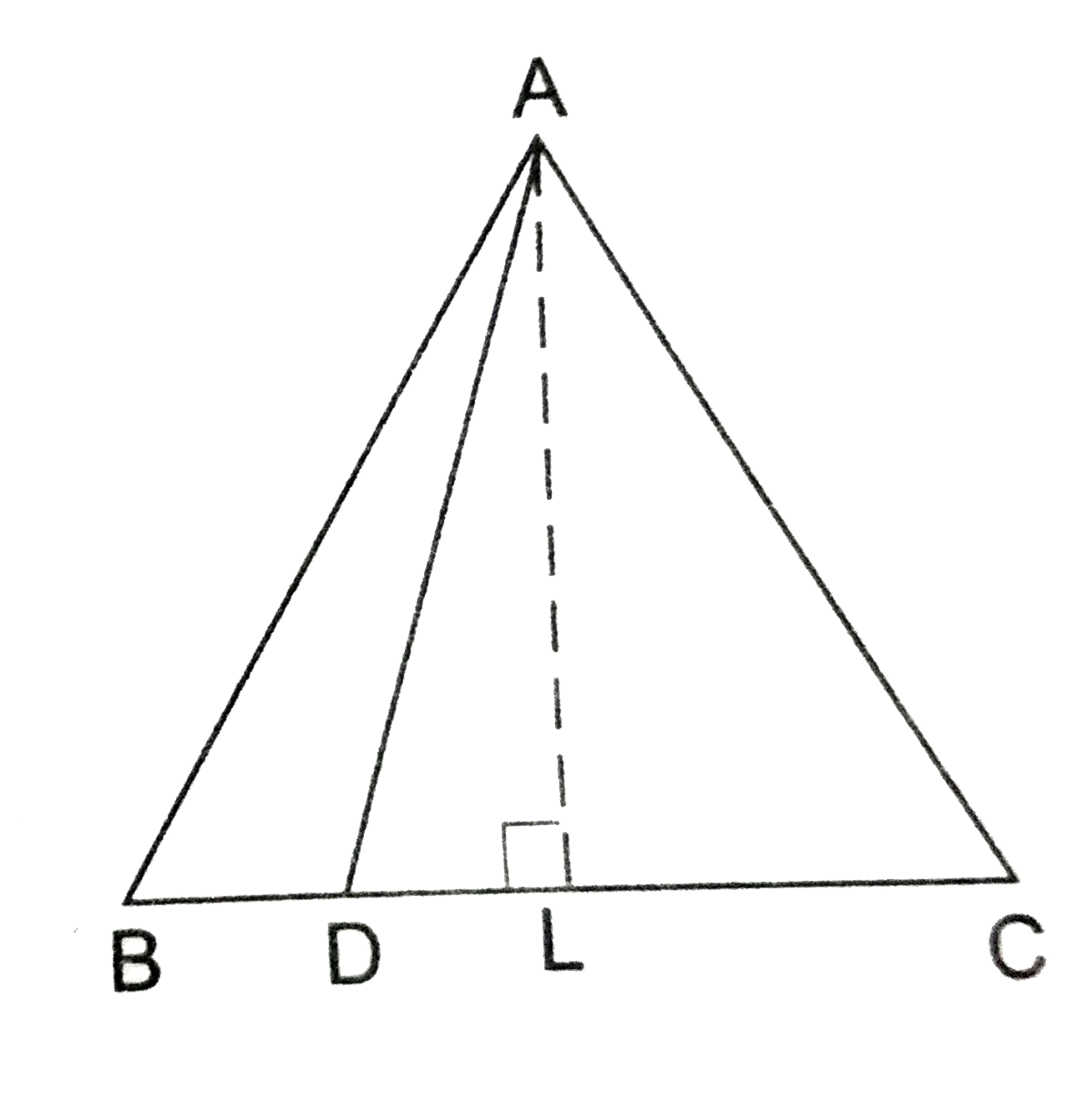
PROOF In right triangles ALB and ALC, we have $A B = A C$ (given) and AL= AL ( common)
$∴ Δ A L B ≅ Δ A L C$ [ by RHS- axiom]
So, BL= CL.
Thus, $B D = \frac{1}{3} B C and B L = \frac{1}{3} B C$ .
In $Δ A L B, ∠ A L B = 90^{\circ}$
$∴ A B^{2} = A L^{2} + B L^{2} . . (i)$ [ by Pythagora's theorem]
In $Δ A L D, ∠ A L D = 90^{\circ}$
$∴ A D^{2} = A L^{2} + D L^{2}$ [ by Pythagora's theorem] ltbr? $= A L^{2} + {(B L - B D)}^{2}$
$= A L^{2} + B L^{2} + B D^{2} - 2 B L \cdot B D$
$= (A L^{2} + B L^{2}) + B D^{2} - 2 B L \cdot B D$
$= A B^{2} + B D^{2} - 2 B L \cdot B D$ [ using (i)]
$= B C^{2} + {(\frac{1}{3} B C)}^{2} - 2 (\frac{1}{2} B C) \cdot \frac{1}{3} B C [∴ A B = B C, B D = \frac{1}{3} B C and B L = \frac{1}{2} B C]$
$= B C^{2} + \frac{1}{9} B C^{2} - \frac{1}{3} B C^{2}$
$= \frac{7}{9} B C^{2} = \frac{7}{9} A B^{2} [∴ B C = A B]$
Hence, $9 A D^{2} = A B^{2}$

Updated on:21/07/2023