In an isosceles triangle ABC, the coordinates of the points Band C on the base BC are respectively (1,2) and (2.1). If the equation of the line AB is y=2x, then the equation of the line AC is
y=12(x−1)
y=x2
y=x−1
2y=x+3
The correct Answer is:B
To find the equation of line AC in the isosceles triangle ABC, we will follow these steps:
Step 1: Identify the coordinates of points B and C
The coordinates of points B and C are given as:
- B(1,2)
- C(2,1)
Step 2: Determine the coordinates of point A
Since triangle ABC is isosceles, the distances from point A to points B and C must be equal. We can express point A in terms of its coordinates. Let's denote the coordinates of point A as A(a,2a).
Step 3: Set up the distance equations
Using the distance formula, the distance from A to B must equal the distance from A to C:
AB=AC
Calculating AB:
AB=√(a−1)2+(2a−2)2
Calculating AC:
AC = \sqrt{(a - 2)^2 + (2a - 1)^2
Setting these distances equal gives us:
√(a−1)2+(2a−2)2=√(a−2)2+(2a−1)2
Step 4: Square both sides to eliminate the square root
Squaring both sides results in:
(a−1)2+(2a−2)2=(a−2)2+(2a−1)2
Step 5: Expand both sides
Expanding both sides:
(a2−2a+1)+(4a2−8a+4)=(a2−4a+4)+(4a2−4a+1)
This simplifies to:
5a2−10a+5=5a2−8a+5
Step 6: Simplify the equation
Subtract 5a2+5 from both sides:
−10a=−8a
This leads to:
−2a=0⟹a=0
Thus, the coordinates of point A are:
A(0,0)
Step 7: Find the slope of line AC
Now we need to find the slope of line AC. The coordinates of points A and C are:
- A(0,0)
- C(2,1)
The slope m of line AC is given by:
m=y2−y1x2−x1=1−02−0=12
Step 8: Write the equation of line AC
Using the point-slope form of the line equation y−y1=m(x−x1):
y−1=12(x−2)
Expanding this gives:
2y−2=x−2
Rearranging to the standard form:
2y=x
Thus, the equation of line AC is:
y=12x
Final Answer
The equation of line AC is:
y=12x
The coordinates of points B and C are given as:
- B(1,2)
- C(2,1)
Since triangle ABC is isosceles, the distances from point A to points B and C must be equal. We can express point A in terms of its coordinates. Let's denote the coordinates of point A as A(a,2a).
Using the distance formula, the distance from A to B must equal the distance from A to C:
AB=AC
Calculating AB:
AB=√(a−1)2+(2a−2)2
Calculating AC:
AC = \sqrt{(a - 2)^2 + (2a - 1)^2
Setting these distances equal gives us:
√(a−1)2+(2a−2)2=√(a−2)2+(2a−1)2
Squaring both sides results in:
(a−1)2+(2a−2)2=(a−2)2+(2a−1)2
Expanding both sides:
(a2−2a+1)+(4a2−8a+4)=(a2−4a+4)+(4a2−4a+1)
This simplifies to:
5a2−10a+5=5a2−8a+5
Subtract 5a2+5 from both sides:
−10a=−8a
This leads to:
−2a=0⟹a=0
Thus, the coordinates of point A are:
A(0,0)
Now we need to find the slope of line AC. The coordinates of points A and C are:
- A(0,0)
- C(2,1)
m=y2−y1x2−x1=1−02−0=12
Using the point-slope form of the line equation y−y1=m(x−x1):
y−1=12(x−2)
Expanding this gives:
2y−2=x−2
Rearranging to the standard form:
2y=x
Thus, the equation of line AC is:
y=12x
The equation of line AC is:
y=12x
Topper's Solved these Questions
- STRAIGHT LINEBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Comprehension Type
3 Videos
- STRAIGHT LINEBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- STATISTICSBOOK - CENGAGE ENGLISHCHAPTER - STATISTICSEXERCISE - Archives
10 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
Similar Questions
The equation of line l1 is y=2x+3, and the equation of line l2 is y=2x-5.
View SolutionIf the ends of the base of an isosceles triangle are at (2, 0) and (0, 1), and the equation of one side is x=2, then the orthocenter of the triangle is
View SolutionThe equation of the image of line y=x wire respect to the line mirror 2x−y=1 is
View SolutionABC is an isosceles triangle. If the coordinates of the base are B(1,3) and C(−2,7) , the coordinates of vertex A
View SolutionABC is an isosceles triangle. If the coordinates of the base are B(1, 3) and C(-2, 7). The coordinates of vertex A can be
View SolutionIn the given figure ABC is a triangle and BC is parallel to the Y-axis. AB and AC intersects the y-axis at Pand Q respectively.
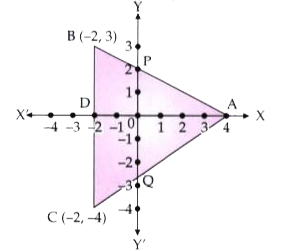
(iv) Find the equation of the line AC.
View SolutionIf the coordinates of the points A,B,C be (−1,5),(0,0) and (2,2) respectively, and D be the middle point of BC, then the equation of the perpendicular drawn from B to the line AD is
View SolutionIn isosceles triangle ABC, D is a point on the base BC produced. Prove that AD>AB.

View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.

Find the equation of the line AC.
View SolutionThe equation of the line AB is y=x. If A and B lie on the same side of the line mirror 2x−y=1, then the equation of the image of AB is
View Solution
