In any triangle ABC, prove that AB2+AC2=2(AD2+BD2) , where D is the midpoint of BC.
Video Solution
Text Solution
Let point B and C lie on the x-axis such that BD=DC, where, D(0,0) is midpoint of BC.
Let point A be (x,y).
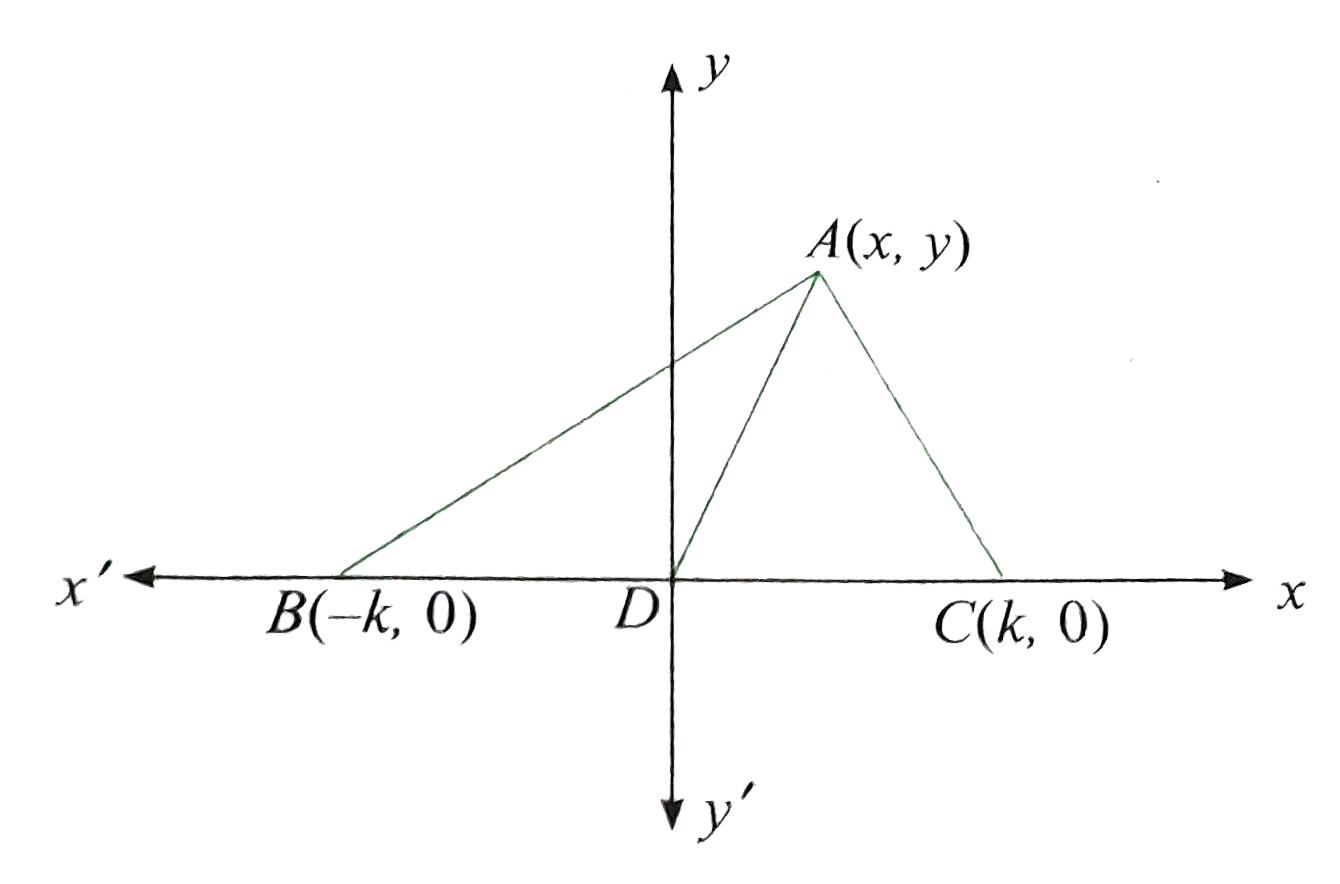
BD=k.So, point B is (−k,0) and point C is (k,0).
Now, AB2+AC2=(x+k)2+(y−0)2+(x−k)2+(y−0)2
=x2+k2+2xk+y2+x2k2−2xk+y2
=2x2+2y2+2k2=2(x2+y2+k2)
And 2(AD2+BD2)=2[(x−0)2+(y−0)2+k2]
=2(x2+y2+k2)
Therefore, AB2+AC2=2(AD2+BD2)
|
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.1
6 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.2
8 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Knowledge Check
In a triangle ABC, it is known that AB=AC. Suppose D is the mid-point of AC and BD=BC=2. Then the area of the triangle ABC is-
A2B2√2C√7D2√7
Prove that the resultant of the vectors represented by the sides −−→AB and −−→AC of a triangle ABC is 2−−→AD, where D is the mid - point of [BC].
View SolutionIn △ABC,if AB=√2,AC=√20,B=(3,2,0),C=(0,1,4) and D is the midpoint of BC then AD=
View SolutionIn quadrilatcal ABCD, prove that AB+BC+CD+AD<2(BD+AC)
View SolutionIn a ΔABC,∠B is an acute-angle and AD⊥BC
Prove that :
(i) AC2=AB2+BC2−2BC×BD
(ii) AB2+CD2=AC2+BD2
View SolutionIn Figure 2,AD⊥BC. Prove that AB2+CD2=BD2+AC2.
View SolutionIn right-angled triangle ABC in which ∠C=90∘ , if D is the mid-point of BC , prove that AB2=4 AD2−3 AC2 .
View SolutionIn the given figure if AD ⊥ BC prove that AB2+CD2=BD2+AC2
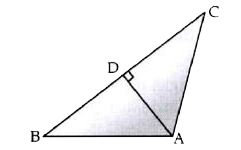
View Solution
