In C0,C1C2….Cn are the binomial coefficients in the expansion of (1+x)n then prove that :
(i)C20−C21+C22−C23+…..+(−1)n.C2n
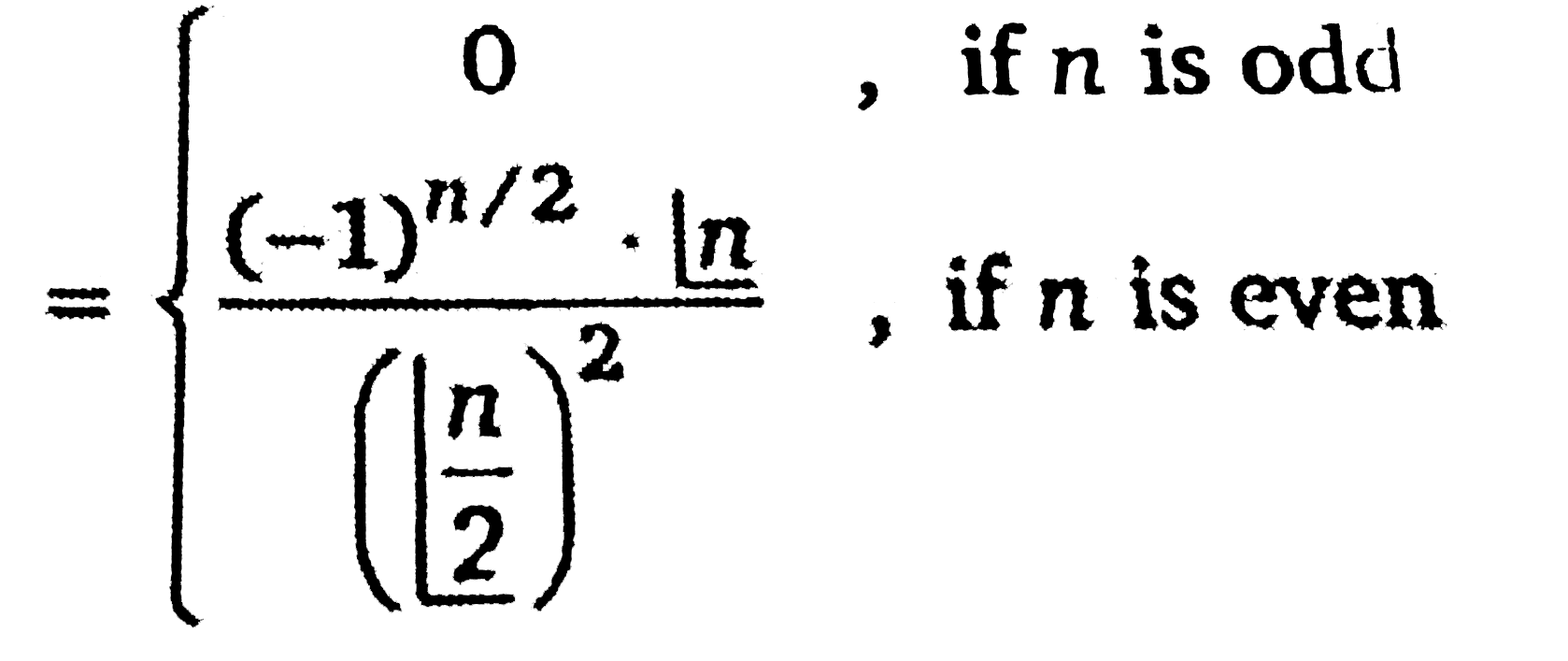
(ii)C0C1+C1C2+C2C3+....+Cn−1Cn
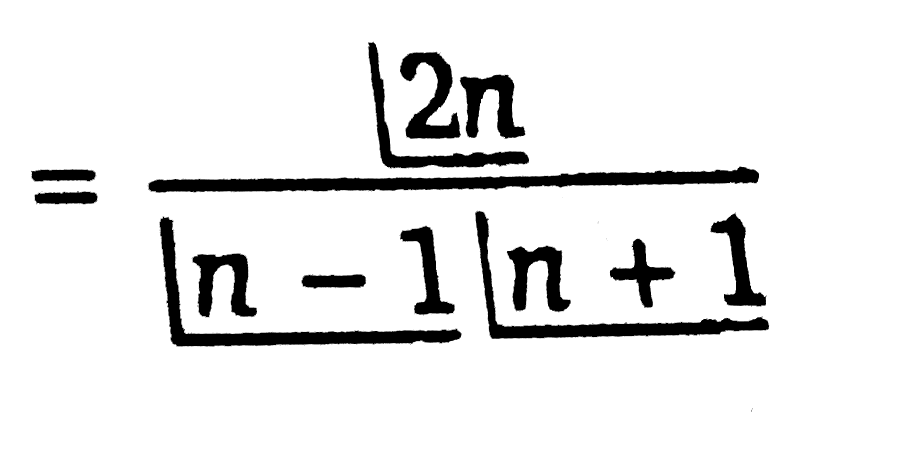
N/a
Topper's Solved these Questions
- BINOMIAL THEOREMBOOK - NAGEEN PRAKASHANCHAPTER - BINOMIAL THEOREMEXERCISE - Exercise 8E
20 Videos
- BINOMIAL THEOREMBOOK - NAGEEN PRAKASHANCHAPTER - BINOMIAL THEOREMEXERCISE - Exercise 8F
20 Videos
- BINOMIAL THEOREMBOOK - NAGEEN PRAKASHANCHAPTER - BINOMIAL THEOREMEXERCISE - Exercise 8C
28 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATION BOOK - NAGEEN PRAKASHANCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATION EXERCISE - MISCELLANEOUS EXERCISE
20 Videos
Similar Questions
In C0,C1C2….Cn are the binomial coefficients in the expansion of (1+x)n then prove that :
(i)C20−C21+C22−C23+…..+(−1)n.C2n
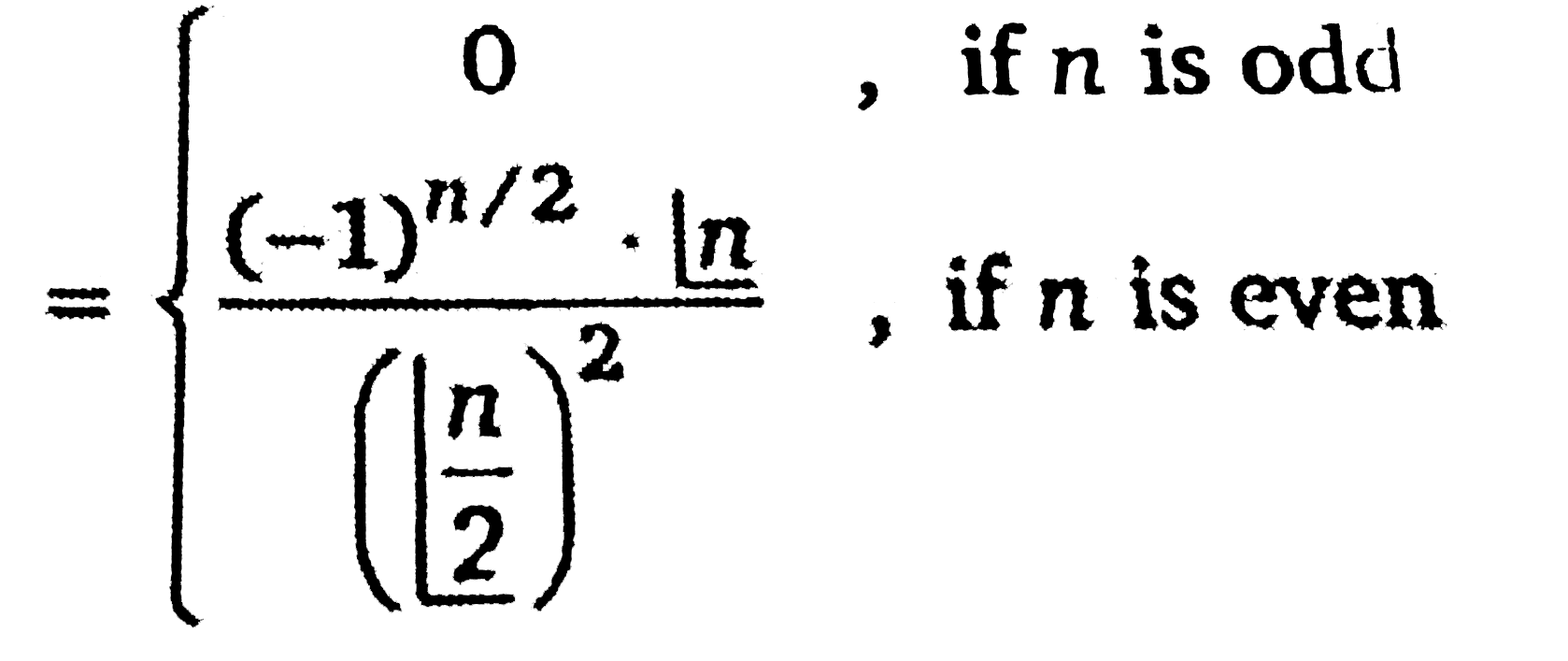
(ii)C0C1+C1C2+C2C3+....+Cn−1Cn
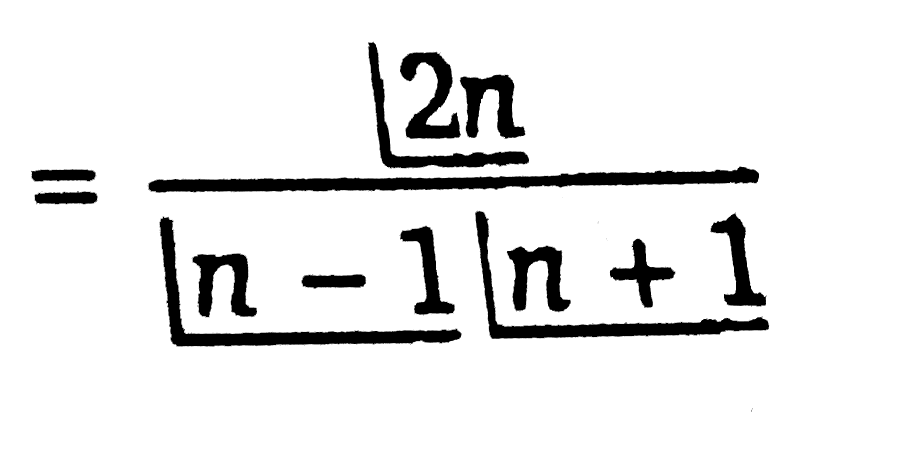
View SolutionIf C0,C1,C2………Cn are the binomial coefficient in the expansion of (1+x)n then prove that:
C20+C21+C22+……..+C2n=∣2–n|n––|n––
View Solution
Knowledge Check
If C0,C1,C2,...,Cn are binomial coefficients
in the expansion of (1+x)n, then the value of
C0−C12+C23−C34+...+(−1)nCnn+1 isA0B1n+1C22n+1D−1n+1If C0,C1,C2,…,Cn denote the binomial coefficients
in the expansion of (1+x)n, then
C02+2C12+3C22+...+(n+1)Cn2=A(2n+1)2nCnB(2n−1)2nCnC(n2+1)2nCnD(n2+1)2n−1CnIf C0,C1C2 ….., denote the binomial coefficients
in the expansion of (1+x)n , then
C02−C13+C24−C35+...+(−1)nCnn+2=A1n+1B1n+2C1n(n+1)D1(n+1)(n+2)
If C0,C1,C2………Cn are the binomial coefficient in the expansion of (1+x)n then prove that:
C20+C21+C22+……..+C2n=∣2–n|n––|n––
View SolutionIf C0,C1,C2,...Cn are the binomial coefficients in the expansion of (1+x)n then prove that: C0+C12+C23+……+Cnn+1=2n+1−1n+1
View SolutionifC0C1C2,……Cn are the binomial coefficients in the expansion of (1+x)n then prove that:
C0C2+C1C3+C2C4+……+Cn−2Cn=∣2–n|n––−2|n––+2
View SolutionifC0C1C2,……Cn are the binomial coefficients in the expansion of (1+x)n then prove that:
C0C2+C1C3+C2C4+……+Cn−2Cn=∣2–n|n––−2|n––+2
View SolutionIf C0,C1,C2,...,Cn denote the binomial coefficientsin the expansion of (1+x)n, then C02−C13+C24−C35+........+(−1)nCnn+2=
View Solution
