In Calculating the mean of grouped data, grouped in classes of equal width, we may use the formula
¯x=a+∑fidi∑fi
Where, a is the assumed mean, a must be one of the mid point of the classes. Is the last statement correct? Justify your answer.
To determine whether the statement "a must be one of the midpoints of the classes" is correct, we need to analyze the formula for calculating the mean of grouped data:
¯x=a+∑fidi∑fi
Where:
- ¯x is the mean of the grouped data.
- a is the assumed mean.
- fi is the frequency of the ith class.
- di is the deviation of the midpoints of the classes from the assumed mean a.
1. Understanding the Assumed Mean:
- The assumed mean a is a value we choose to simplify calculations. It does not necessarily have to be a midpoint of any class.
2. Role of the Assumed Mean:
- The purpose of the assumed mean is to provide a reference point from which we can calculate deviations di. These deviations are calculated as the difference between the midpoints of the classes and the assumed mean a.
3. Can a Be Any Value?:
- Yes, a can be any value that makes the calculations easier. It is often chosen to be close to the actual mean, but it is not restricted to being a midpoint of any class.
4. Conclusion:
- Since a does not have to be one of the midpoints of the classes, the statement "a must be one of the midpoints of the classes" is false.
Justification:
- The statement is false because the assumed mean a can be any value that simplifies the calculation. It does not need to be a midpoint of the classes. The choice of a is flexible and can be based on convenience.
- ¯x is the mean of the grouped data.
- a is the assumed mean.
- fi is the frequency of the ith class.
- di is the deviation of the midpoints of the classes from the assumed mean a.
- The assumed mean a is a value we choose to simplify calculations. It does not necessarily have to be a midpoint of any class.
- The purpose of the assumed mean is to provide a reference point from which we can calculate deviations di. These deviations are calculated as the difference between the midpoints of the classes and the assumed mean a.
- Yes, a can be any value that makes the calculations easier. It is often chosen to be close to the actual mean, but it is not restricted to being a midpoint of any class.
- Since a does not have to be one of the midpoints of the classes, the statement "a must be one of the midpoints of the classes" is false.
- The statement is false because the assumed mean a can be any value that simplifies the calculation. It does not need to be a midpoint of the classes. The choice of a is flexible and can be based on convenience.
Topper's Solved these Questions
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - SHORT ANSWERS QUESTIONS
42 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ASWERS QUESTIONS
14 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ASWERS QUESTIONS
14 Videos
- REAL NUMBERSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - REAL NUMBERSEXERCISE - LONG ANSWER TYPE QUESTIONS
5 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS
20 Videos
Similar Questions
In the formula ¯x=a+∑fidi∑fi
for finding the mean of grouped data di'S and deviation from a of
View SolutionIn the formula ¯x=a+h∑fiui∑fi
for finding the mean of grouped frequency distribution ui is equal to
View SolutionIf xi's are the mid-points of the class intervals of grouped data, fi's are the corresponding frequencies and ¯x is the mean, then ∑(fixi−¯x) equal to
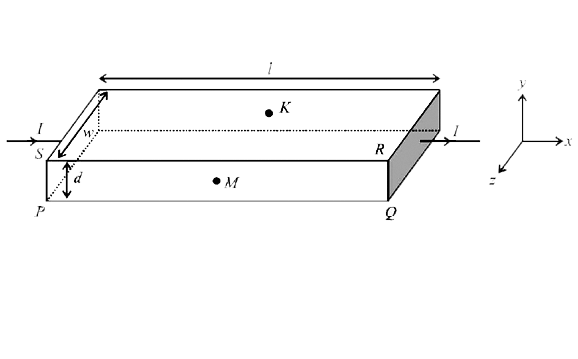
View SolutionIn a thin rectangular metallic strip a constant current I flows along the positive x−direction , as shown in the figure. The length , width and thickness of the strip are l,wandd, respectively.
A uniform magnetic field →B is applied on the strip along the positive y−direction . Due to this, the charge carriers experience a net deflection along the z−direction . This results in accumulation of charge carriers on the surface PQRS ansd apperance of equal and opposite charges on the face opposite to PQRS. A potential difference along the z−direction is thus developed. Charge accumulation contiues untill the magnetic force is balanced by the electric force. The current is assumed to be uniformly distributed on the cross- section of the strip and carried by electrons.
Consider two different metallic strips (1and2) of the same material . Their lengths are the same,widths are w1andw2 and thickness are d1andd2 respectively. Two points KandM are symmetrically located on the opposite faces parallel to the x−y plane ( see figure) . V1andV2 are the potential differences between KandM in strips 1and2, respectively . Then, for a given current I flowing through them in a given magnetic field strength B, the correct statement(s) is (are)
View SolutionIn a thin rectangular metallic strip a constant current I flows along the positive x−direction , as shown in the figure. The length , width and thickness of the strip are l,wandd, respectively.
A uniform magnetic field →B is applied on the strip along the positive y−direction . Due to this, the charge carriers experience a net deflection along the z−direction . This results in accumulation of charge carriers on the surface PQRS ansd apperance of equal and opposite charges on the face opposite to PQRS. A potential difference along the z−direction is thus developed. Charge accumulation contiues untill the magnetic force is balanced by the electric force. The current is assumed to be uniformly distributed on the cross- section of the strip and carried by electrons.
Consider two different metallic strips (1and2) of the same material . Their lengths are the same,widths are w1andw2 and thickness are d1andd2 respectively. Two points KandM are symmetrically located on the opposite faces parallel to the x−y plane ( see figure) . V1andV2 are the potential differences between KandM in strips 1and2, respectively . Then, for a given current I flowing through them in a given magnetic field strength B, the correct statement(s) is (are)

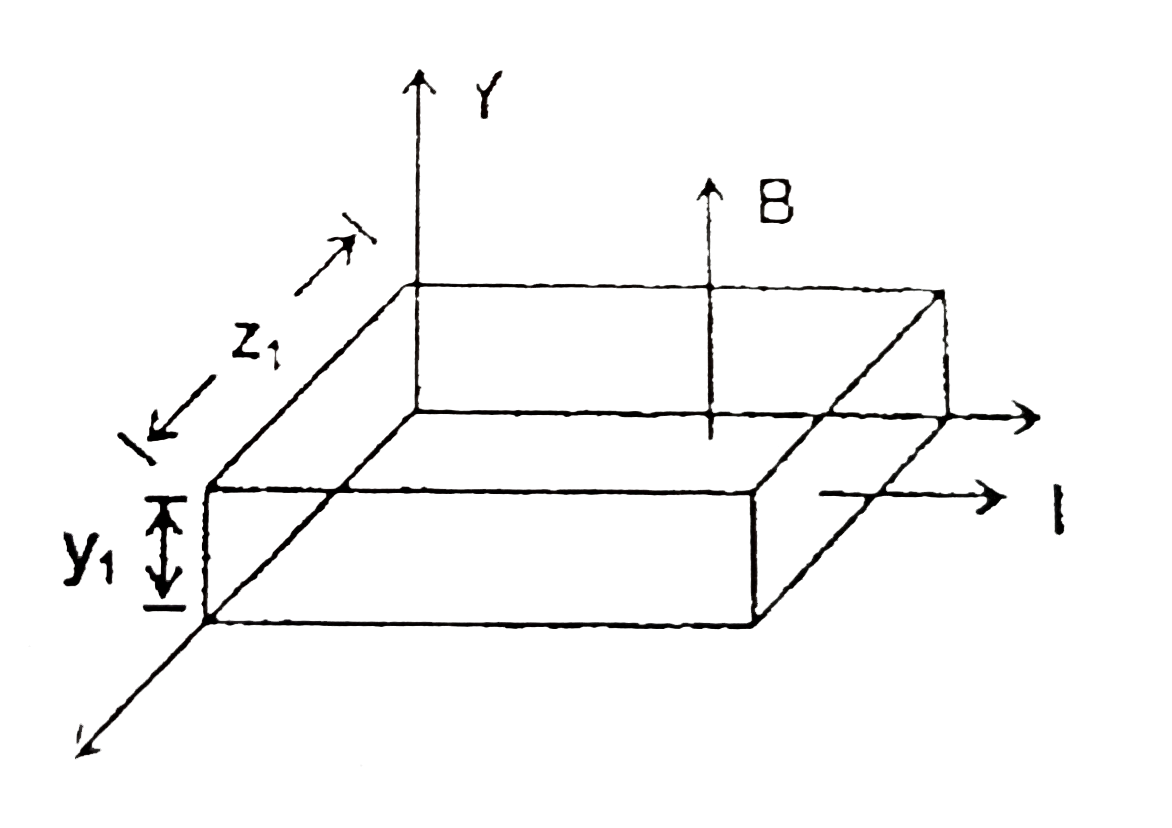
View SolutionThe basic principle underlying the Hall effect is the Lorentz force. When an electron moves along a direction perpendicular to an applied magnetic field, it experiences a force acting normal to both the directions and moves in response to this force and the force exerted by the internal electric field. For an n-type, bar-shaped semiconductor, the carriers are predominantly electrons of bulk density n. We assume that the constant current I flows along the x-axis from left to right in the presence of a magnetic field toward y-axis. Electrons subjected to the lorentz force initially drift away from the current line toward the negative z-axis, resulting in an excess surface electrical charge on the sides of the sample. This charge results in the hall voltage, a potential drop across the two sides of the sample.
The transverse voltage is the hall voltage VH and its magnitude is equal to IB/qnd, where I is the current, B is the magnetic field, d is the sample thickness and q is the elementary charge. A silver ribbon lies as shown in the adjacent figure. (z1=11.8mm and y1=0.23mm) carrying a current of 120A in the x-direction in a uniform magnetic field B=0.95T. If electron density is 5.85×1028/m3, then
Magnitude of the drift velocity of elelctrons is
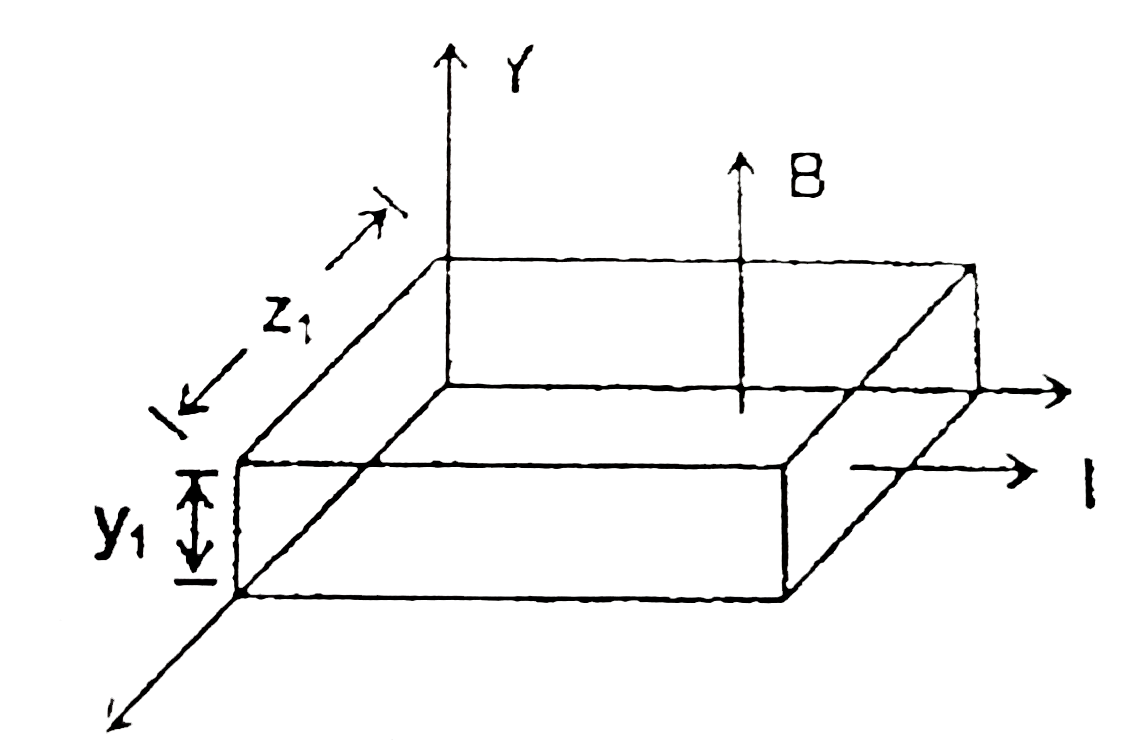
View SolutionThe basic principle underlying the Hall effect is the Lorentz force. When an electron moves along a direction perpendicular to an applied magnetic field, it experiences a force acting normal to both the directions and moves in response to this force and the force exerted by the internal electric field. For an n-type, bar-shaped semiconductor, the carriers are predominantly electrons of bulk density n. We assume that the constant current I flows along the x-axis from left to right in the presence of a magnetic field toward y-axis. Electrons subjected to the lorentz force initially drift away from the current line toward the negative z-axis, resulting in an excess surface electrical charge on the sides of the sample. This charge results in the hall voltage, a potential drop across the two sides of the sample.
The transverse voltage is the hall voltage VH and its magnitude is equal to IB/qnd, where I is the current, B is the magnetic field, d is the sample thickness and q is the elementary charge. A silver ribbon lies as shown in the adjacent figure. (z1=11.8mm and y1=0.23mm) carrying a current of 120A in the x-direction in a uniform magnetic field B=0.95T. If electron density is 5.85×1028/m3, then
What is the value of hall emf ?
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
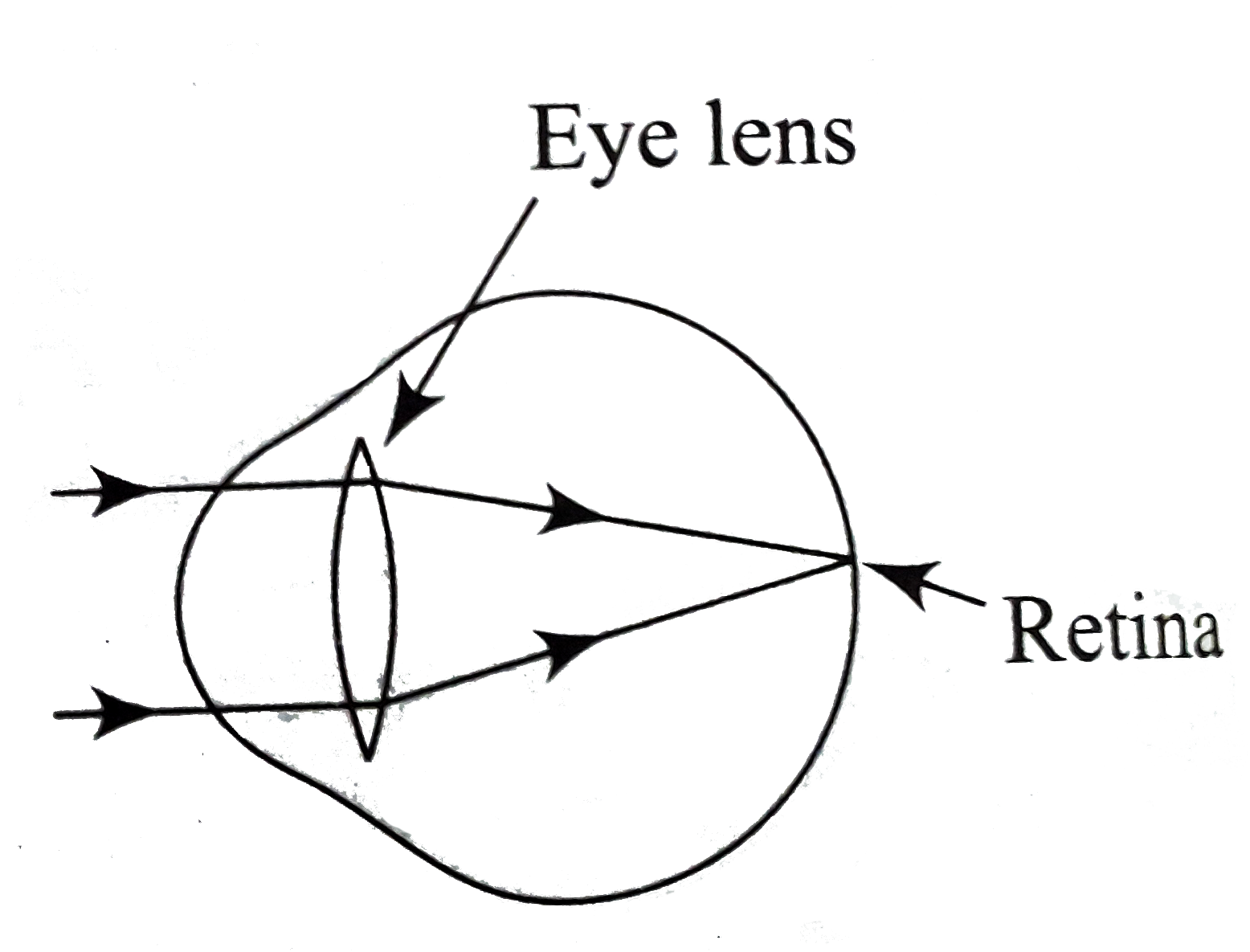
Q. A person can see objects clearly from distance 10cm to ∞. Then, we can say that the person is
View SolutionRam and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
Sign of work done by the camel on the load during parts of motion, accelerated motion, uniform motion and retarded motion, respectively are
View SolutionRam and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
The ratio of the energy consumed by the camel during uniform motion for the two cases when it moves with speed 5ms−1 to the case when it moves with 10ms−1
View Solution
