In cm then BD is equal to
cm
cm
cm
cm
To solve the problem, we need to find the length of BD in triangle ABC where angle B is 90 degrees, AC = 9 cm, and AD = 3 cm. Here are the step-by-step calculations:
Step 1: Understand the Triangle
In triangle ABC, angle B is 90 degrees. We have points A, B, and C with AC being the hypotenuse. BD is perpendicular to AC.
Step 2: Identify the Lengths
Given:
- AC = 9 cm
- AD = 3 cm
Since AC = AD + DC, we can find DC:
DC=AC−AD=9 cm−3 cm=6 cm
Step 3: Apply the Pythagorean Theorem
We will use the Pythagorean theorem in two triangles: ABD and BDC.
1. In triangle ABD:
- Hypotenuse = AB
- Base = AD = 3 cm
- Perpendicular = BD
By Pythagorean theorem:
AB2=AD2+BD2
AB2=32+BD2
AB2=9+BD2 (Equation 1)
2. In triangle BDC:
- Hypotenuse = BC
- Base = DC = 6 cm
- Perpendicular = BD
By Pythagorean theorem:
BC2=BD2+DC2
BC2=BD2+62
BC2=BD2+36 (Equation 2)
Step 4: Use Triangle ABC
In triangle ABC:
- Hypotenuse = AC = 9 cm
- Base = AB
- Height = BC
Using the Pythagorean theorem:
AC2=AB2+BC2
92=AB2+BC2
81=AB2+BC2 (Equation 3)
Step 5: Substitute Equations
From Equations 1 and 2, we can express AB^2 and BC^2 in terms of BD^2:
- From Equation 1: AB2=9+BD2
- From Equation 2: BC2=BD2+36
Substituting these into Equation 3:
81=(9+BD2)+(BD2+36)
81=9+36+2BD2
81=45+2BD2
81−45=2BD2
36=2BD2
BD2=18
Step 6: Solve for BD
Taking the square root:
BD=√18=√9×2=3√2 cm
Final Answer
Thus, the length of BD is 3√2 cm.
---
In triangle ABC, angle B is 90 degrees. We have points A, B, and C with AC being the hypotenuse. BD is perpendicular to AC.
Given:
- AC = 9 cm
- AD = 3 cm
DC=AC−AD=9 cm−3 cm=6 cm
We will use the Pythagorean theorem in two triangles: ABD and BDC.
- Hypotenuse = AB
- Base = AD = 3 cm
- Perpendicular = BD
AB2=AD2+BD2
AB2=32+BD2
AB2=9+BD2 (Equation 1)
- Hypotenuse = BC
- Base = DC = 6 cm
- Perpendicular = BD
BC2=BD2+DC2
BC2=BD2+62
BC2=BD2+36 (Equation 2)
In triangle ABC:
- Hypotenuse = AC = 9 cm
- Base = AB
- Height = BC
AC2=AB2+BC2
92=AB2+BC2
81=AB2+BC2 (Equation 3)
From Equations 1 and 2, we can express AB^2 and BC^2 in terms of BD^2:
- From Equation 1: AB2=9+BD2
- From Equation 2: BC2=BD2+36
81=(9+BD2)+(BD2+36)
81=9+36+2BD2
81=45+2BD2
81−45=2BD2
36=2BD2
BD2=18
Taking the square root:
BD=√18=√9×2=3√2 cm
Thus, the length of BD is 3√2 cm.
Topper's Solved these Questions
- SAMPLE PAPER 2022BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2022EXERCISE - SECTION C (Case study based questions)
10 Videos
- SAMPLE PAPER 2022BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2022EXERCISE - SECTION C (Case study based questions)
10 Videos
- SAMPLE PAPER (MATHEMATICS STANDARD)BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER (MATHEMATICS STANDARD)EXERCISE - PART - A
15 Videos
- SAMPLE PAPER 2022 TERM IIBOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2022 TERM IIEXERCISE - SECTION C
10 Videos
Similar Questions
In △ABC ,∠ABC=90∘ and BD⊥AC. If AD = 4 cm and CD =5 cm, then BD is equal to:
त्रिभुज ABC में, ∠ABC=90∘ तथा BD⊥AC है | यदि AD =4 सेमी और CD = 5सेमी है, तो BD किसके बराबर है ?
View SolutionIn △ABC, ∠ABC=90∘ and BD⊥AC. if AD=4 cm and CD=5 cm, then BD is equal to:
△ABC में, ∠ABC=90∘ और BD⊥AC है| यदि AD=4 cm और CD=5 cm तो BD किसके समान होगा?
View Solution
Knowledge Check
In ΔABC∠BAC=90∘ and ADI_BC. If BD=3cm and CD=4cm, then the length of AD is
A3.5 cmB5cmC2√3 cmD6cm
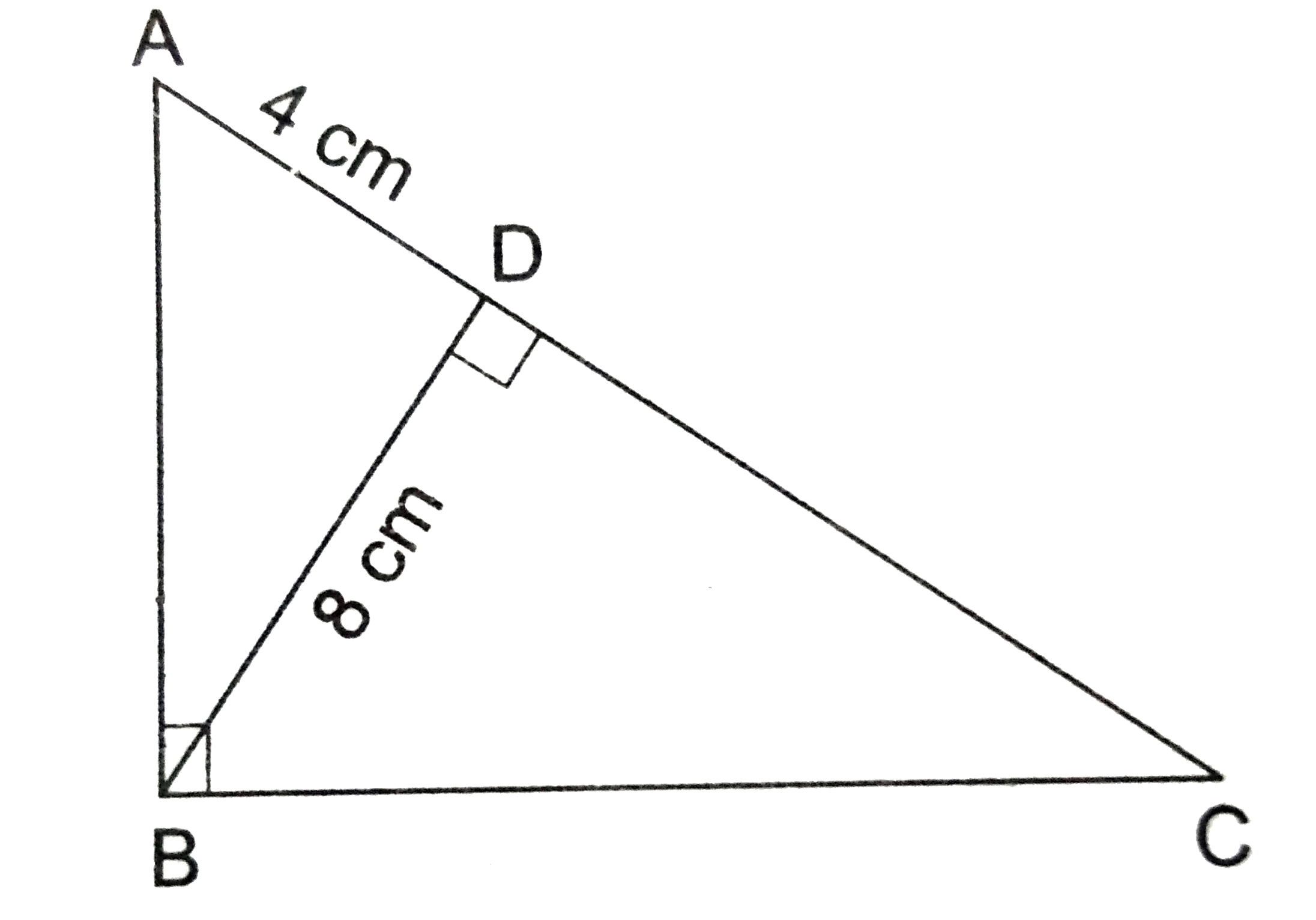
In the given figure, ∠ABC=90∘andBD⊥AC. If BD=8cm,AD=4cm find CD.
View SolutionIn ΔABC,∠B=90∘andBD⊥AC. If AC=17cmandBD=4cm then find the area of rectangle formed by ADandDC.
View SolutionIn a triangle ABC, ∠BCA=90∘ and CD is perpendicular to AB. If AD = 4 cm and BD = 9 cm, then the value of DC will be
View SolutionIn triangle ABC, ∠BAC=90∘andAD⊥BC. If BD = 3 and CD = 4 cm, then the length of AD is.
View SolutionIn the triangle ABC, D is on BC ∠ADB=90∘,∠ABC=45∘, AD= 10cm, AC = 20 cm. then BC is equal to:
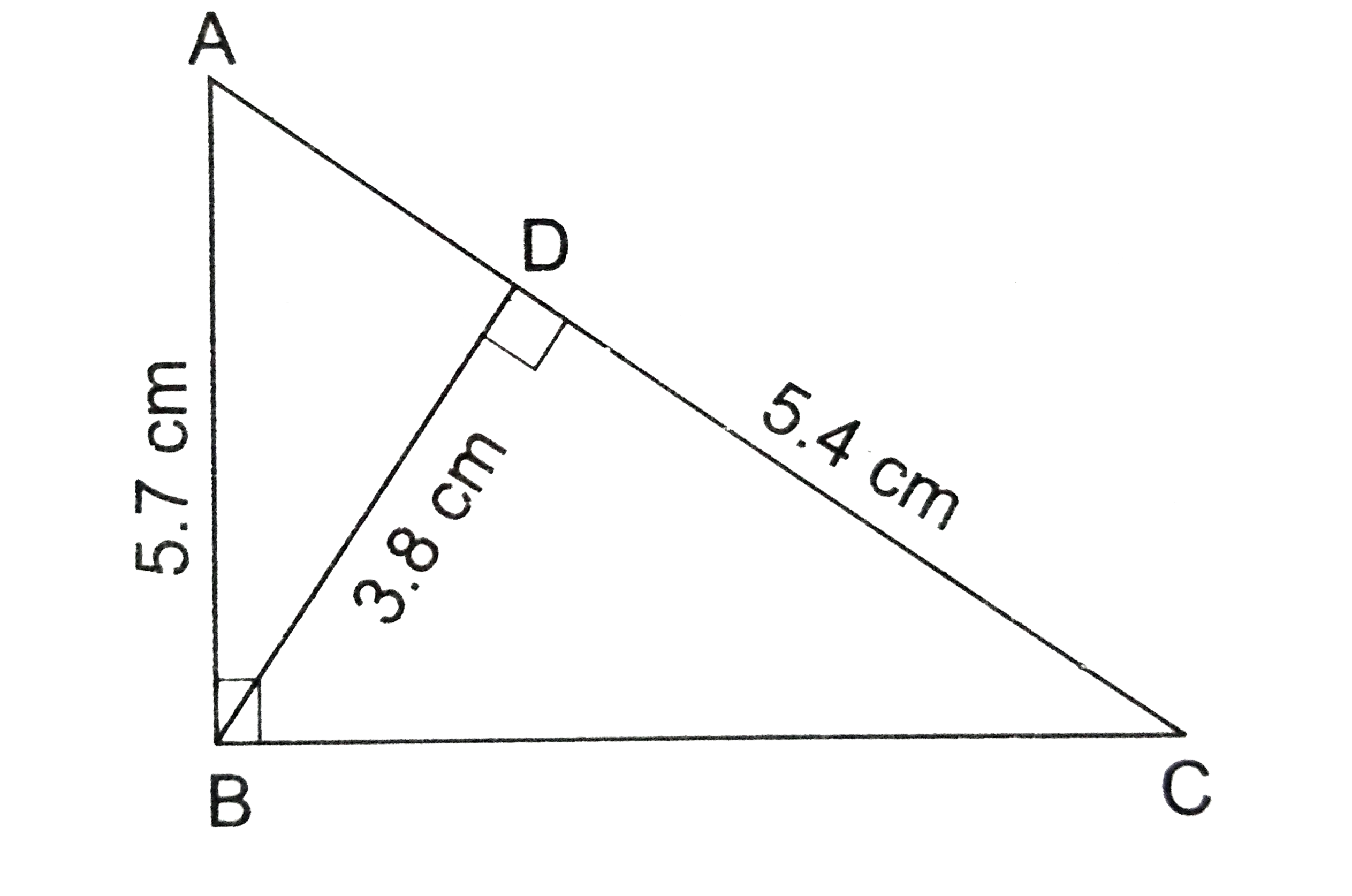
View SolutionIn the given figure, ∠ABC=90∘andBD⊥AC. If AB=5.7cm,BD=3.8cmandCD=5.4cm, find BC.
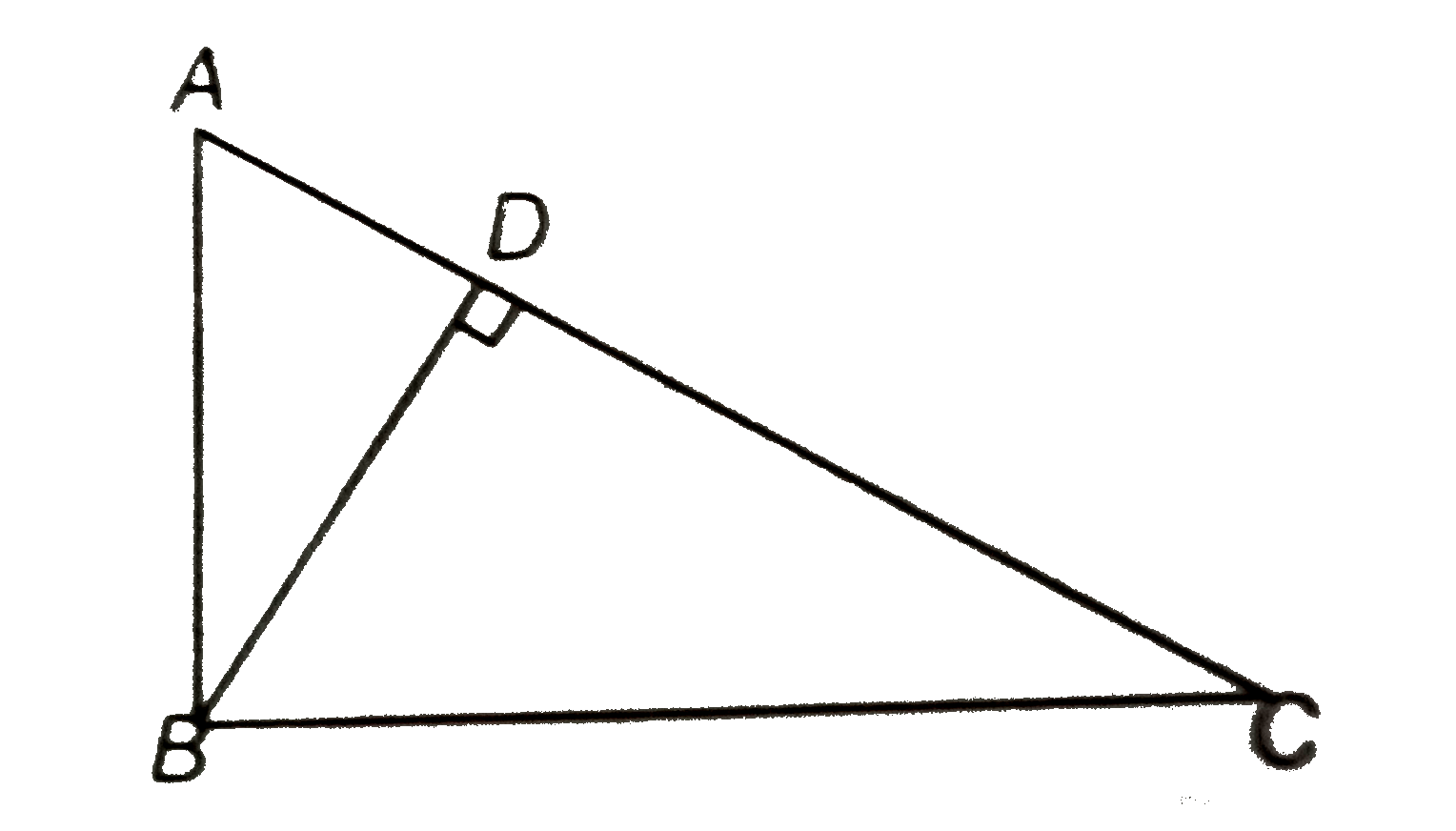
View SolutionIn given figure, ABC is a triangle right angled at B and BD⊥AC. If AD=4 cm and CD= 5 cm, then find BD and AB.
View Solution
