In the triangle ABC, D is on BC ∠ADB=90∘,∠ABC=45∘, AD= 10cm, AC = 20 cm. then BC is equal to:
10 cm
27.32 cm
18.42 cm
14.14 cm
To solve the problem step by step, we will follow the geometric relationships and properties of triangles.
Step 1: Understand the given information
We have triangle ABC with point D on side BC. The following information is provided:
- Angle ADB = 90°
- Angle ABC = 45°
- AD = 10 cm
- AC = 20 cm
Step 2: Draw the triangle
Draw triangle ABC and mark point D on side BC. Label the angles and sides according to the given information.
Step 3: Identify angles in triangle ABD
Since angle ADB is 90° and angle ABC is 45°, we can find angle ABD:
- Angle ADB = 90°
- Angle ABC = 45°
- Therefore, angle ABD = 180° - (90° + 45°) = 45°
Step 4: Recognize triangle properties
In triangle ABD, we have:
- Angle ADB = 90°
- Angle ABD = 45°
- Therefore, angle BAD = 45°
This means triangle ABD is an isosceles right triangle, where AD = BD.
Step 5: Calculate BD
Since AD = 10 cm, we have:
- BD = AD = 10 cm
Step 6: Use the Pythagorean theorem in triangle ADC
Now, we will find DC using triangle ADC. We know:
- AC = 20 cm
- AD = 10 cm
- Angle ADC = 90°
Using the Pythagorean theorem:
DC2+AD2=AC2
Substituting the known values:
DC2+102=202
DC2+100=400
DC2=400−100
DC2=300
DC=√300=√100×3=10√3≈17.32 cm
Step 7: Calculate BC
Now we can find BC:
BC=BD+DC
Substituting the values we found:
BC=10 cm+17.32 cm
BC=27.32 cm
Final Answer
Therefore, the length of BC is 27.32 cm.
---
We have triangle ABC with point D on side BC. The following information is provided:
- Angle ADB = 90°
- Angle ABC = 45°
- AD = 10 cm
- AC = 20 cm
Draw triangle ABC and mark point D on side BC. Label the angles and sides according to the given information.
Since angle ADB is 90° and angle ABC is 45°, we can find angle ABD:
- Angle ADB = 90°
- Angle ABC = 45°
- Therefore, angle ABD = 180° - (90° + 45°) = 45°
In triangle ABD, we have:
- Angle ADB = 90°
- Angle ABD = 45°
- Therefore, angle BAD = 45°
Since AD = 10 cm, we have:
- BD = AD = 10 cm
Now, we will find DC using triangle ADC. We know:
- AC = 20 cm
- AD = 10 cm
- Angle ADC = 90°
DC2+AD2=AC2
Substituting the known values:
DC2+102=202
DC2+100=400
DC2=400−100
DC2=300
DC=√300=√100×3=10√3≈17.32 cm
Now we can find BC:
BC=BD+DC
Substituting the values we found:
BC=10 cm+17.32 cm
BC=27.32 cm
Therefore, the length of BC is 27.32 cm.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In ΔABC,∠B=90∘ and BD⊥AC. If AC = 9 cm and AD = 3 cm, then BD is equal to :
A2√2 cmB3√2 cmC2√3 cmD3√3 cm
In the triangle ABC,∠ABCor∠B=90∘.AB:BD:DC=3:1:3. If AC=20cm , then what is the length of AD (in cm) ?
View SolutionIn △ABC, ∠ABC=90∘ and BD⊥AC. if AD=4 cm and CD=5 cm, then BD is equal to:
△ABC में, ∠ABC=90∘ और BD⊥AC है| यदि AD=4 cm और CD=5 cm तो BD किसके समान होगा?
View SolutionIf △ABC is a right angled triangle with ∠ABC=90∘, and AC = 10 cm and BC = 8 cm, then the length of AB is:
यदि △ABC एक समकोण त्रिभुज है, ∠ABC=90∘,AC =10, BC =8 cm फिर AB की लंबाई है:
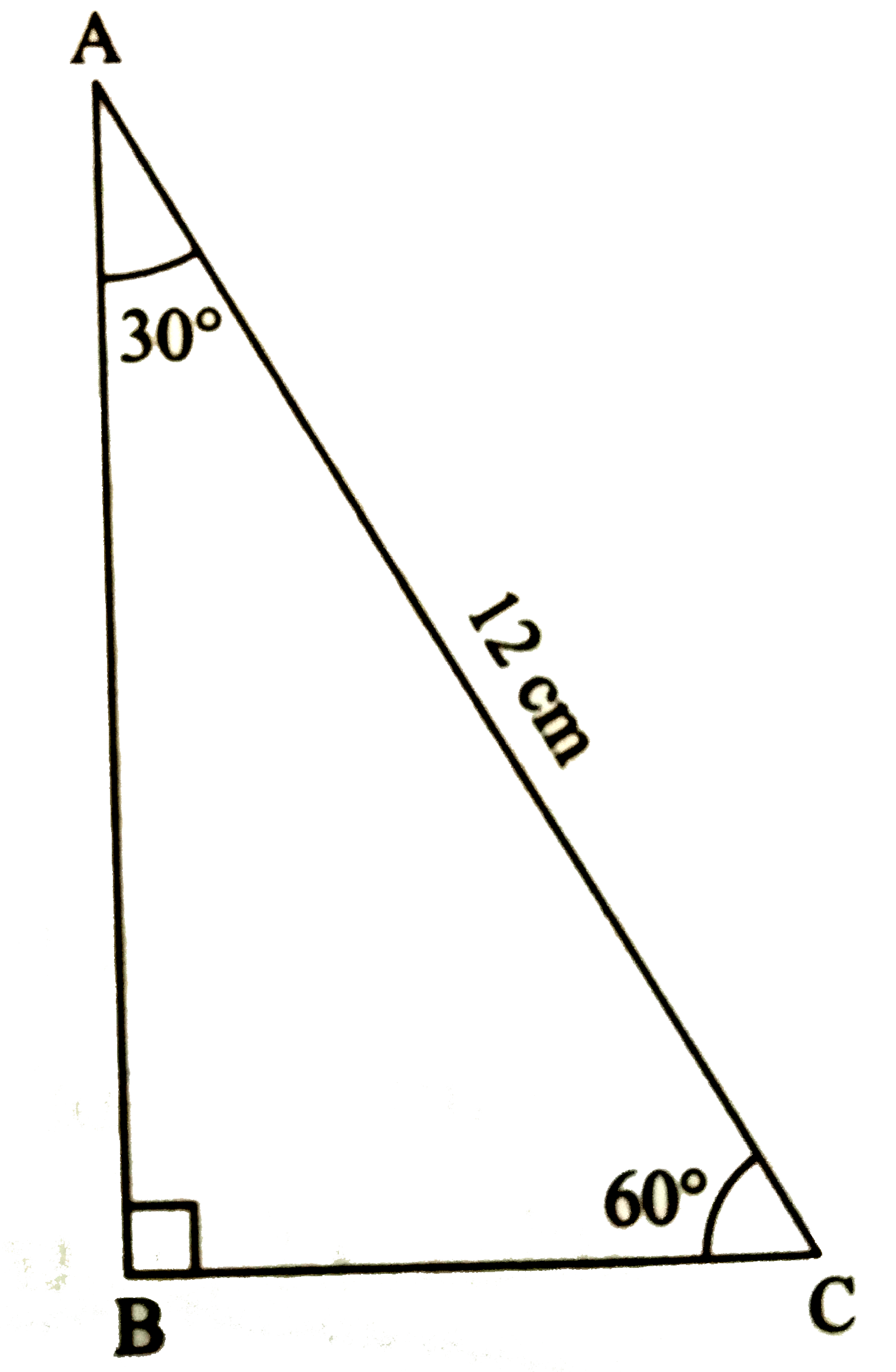
View SolutionIn the figure , AC =12 cm ,
∠ABC=90∘, ∠BAC=30∘ ,
then find AB and BC.
View SolutionIn a right-angled triangle ABC, if angle B=90°, BC = 3 cm and AC = 5 cm, then the length of side AB is
View SolutionIn a ΔABC,∠A=120∘,AB=20cm,AC=30cm find the angle bisector AD .
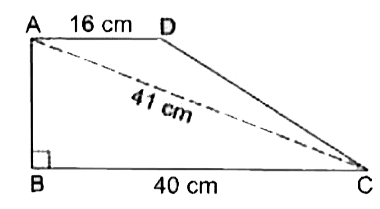
View SolutionIn the given figure, ABCD is a trapezium in which AD∣∣BC,∠ABC=90∘,AD=16cm,AC=41cm and BC = 40 cm. Find the area of the trapezium.
View Solution