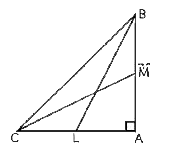
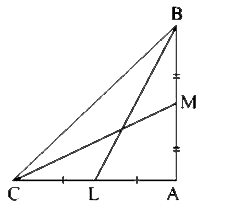
In ΔABC,∠BAC=90∘, seg BL and seg CM are median of ΔABC. Then prove that: 4(Bl2+Cm2)=5BC2
Text Solution
The correct Answer is:4(BL2+Cm2)=5BC2
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - UNIQUE PUBLICATIONCHAPTER - PYTHAGORS THEORMEXERCISE - HOTS-SOLVED5videos
PYTHAGORS THEORM
- BOOK - UNIQUE PUBLICATIONCHAPTER - PYTHAGORS THEORMEXERCISE - UNIQUE PRACTICE SESSION MCQ.S (1 MARKS QUESTION )11videos
PYTHAGORS THEORM
- BOOK - UNIQUE PUBLICATIONCHAPTER - PYTHAGORS THEORMEXERCISE - PRACTICE SET 2.24videos
PYTHAGORS THEORM
- BOOK - UNIQUE PUBLICATIONCHAPTER - PROBABILITY EXERCISE - PROBLEM SET 523videos
PROBABILITY
- BOOK - UNIQUE PUBLICATIONCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNMENT6videos
QUADRATIC EQUATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
In a ΔABC, angle BAC = 90∘. If BC = 25 cm, then what is the length of the median AD ?A24 cmB12.5 cmC14.5 cmD10 cm
seg AN and seg CM are the medians of △ABC in which ∠B=90∘ Prove that 4(AN2+CM2)=5AC2
View SolutionBL and CM are medians of a triangle ABC right angled at A. Prove that 4(BL2+CM2)=5BC2
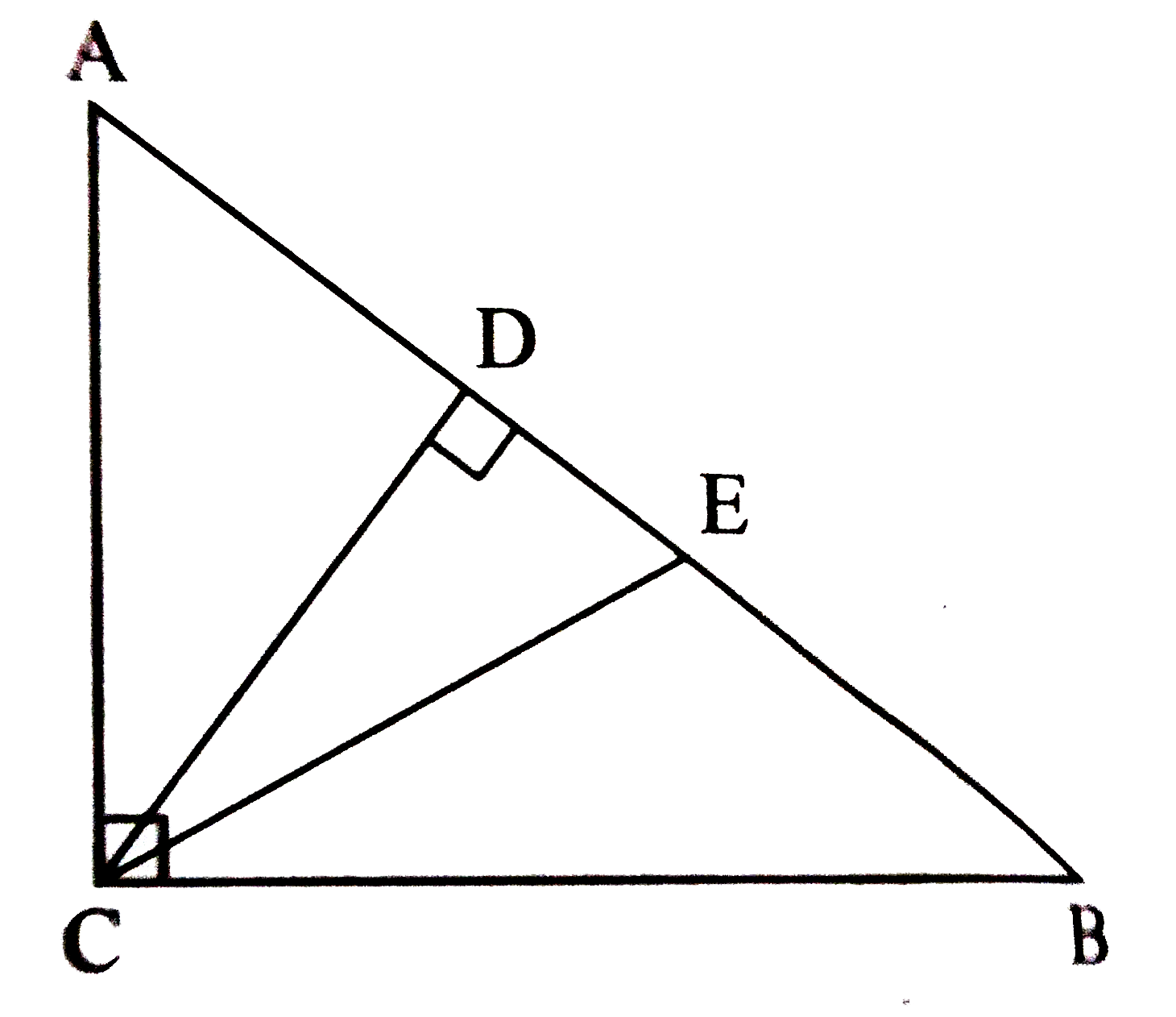
View SolutionIn ΔABC,∠ACB=90∘, seg CD⊥ side AB and seg CE is angle bisector of ∠ACB
Prove : ADBD=AE2BE2
 View Solution
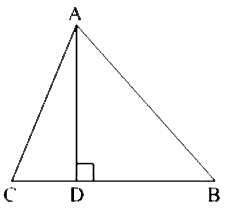
View SolutionIn ΔABC seg AD⊥segBC,DB=3CD Prove that 2AB2=2AC2+BC2
View SolutionIn ΔABC, seg AD⊥ seg BCDB=3CD.
Prove that : 2AB2=2AC2+BC2
 View Solution
View SolutionIn ΔABC,segAd⊥segBC,∠C,=45∘,BD=5andAC=5√2 then find AD and BC.
View SolutionIn △ABC,∠ABC=90∘
∠BAC=45∘ and AC =4√2cm,
then find AB.
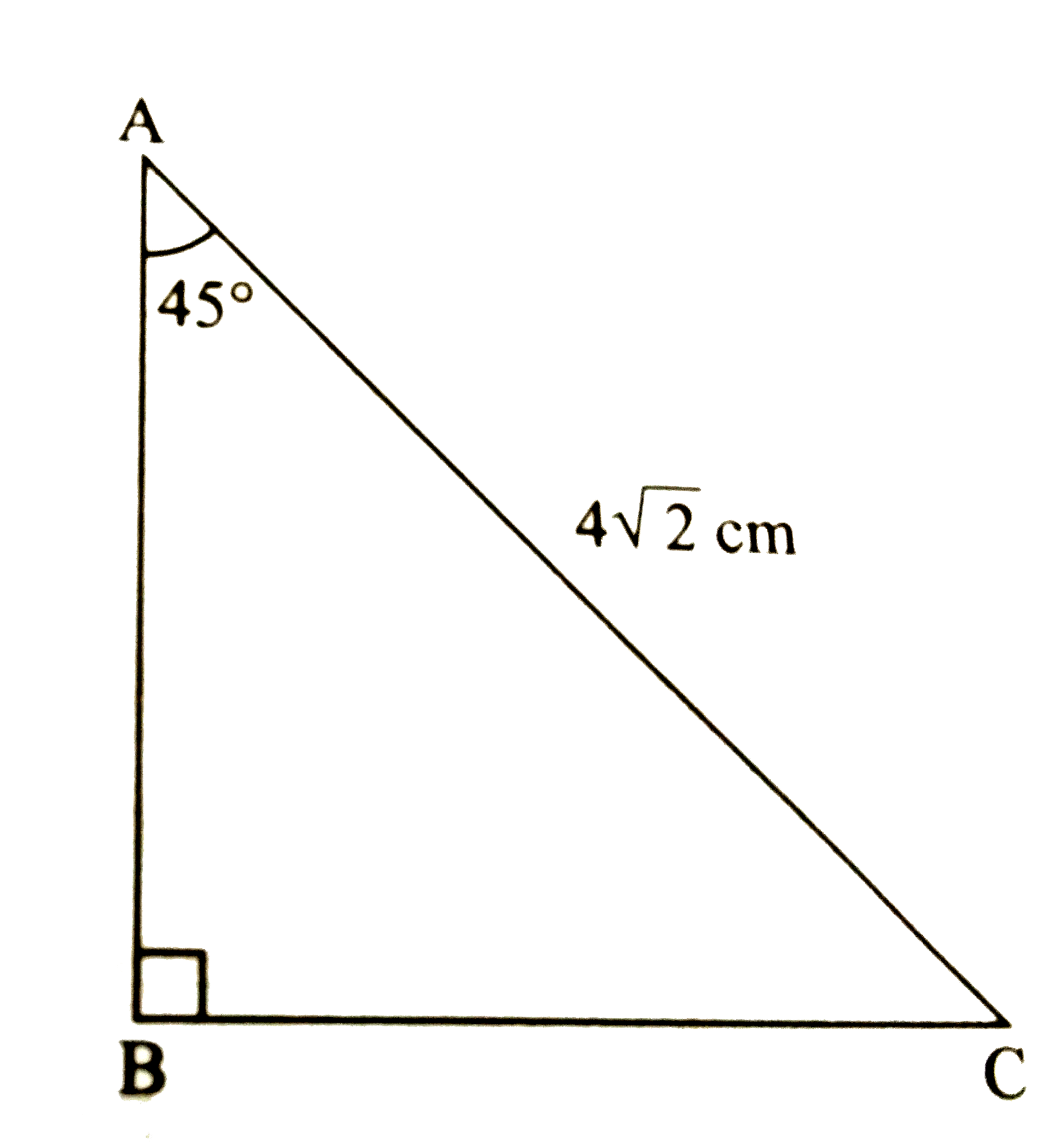 View Solution
View Solution