In the figure ΔPQR is an equilateral triangle. Point S is on seg QR such that
QS=13QR.
Prove that : 9PS2=7PQ2

The correct Answer is:9PS2=7PQ2
Topper's Solved these Questions
- PYTHAGORS THEORMBOOK - UNIQUE PUBLICATIONCHAPTER - PYTHAGORS THEORMEXERCISE - HOTS-SOLVED
5 Videos
- PYTHAGORS THEORMBOOK - UNIQUE PUBLICATIONCHAPTER - PYTHAGORS THEORMEXERCISE - UNIQUE PRACTICE SESSION MCQ.S (1 MARKS QUESTION )
11 Videos
- PYTHAGORS THEORMBOOK - UNIQUE PUBLICATIONCHAPTER - PYTHAGORS THEORMEXERCISE - PRACTICE SET 2.2
4 Videos
- PROBABILITY BOOK - UNIQUE PUBLICATIONCHAPTER - PROBABILITY EXERCISE - PROBLEM SET 5
23 Videos
- QUADRATIC EQUATIONS BOOK - UNIQUE PUBLICATIONCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNMENT
6 Videos
Similar Questions
In the figure 2.35,ΔPQR is an equilatral triangle. Point S is on seg QR such that QS=13QR. Prove that : 9PS2=7PQ2
View SolutionIn the adjoining figure, ΔPQR is an equilateral triangle. Point S is on seg QR. such that QS=13QR. Prove that : 9PS2=7PQ2.
View Solution1. In the figure △PQR is an equilateral triangle, the point N is on ray QR such that QR=RN. Prove that PN2=3PR2
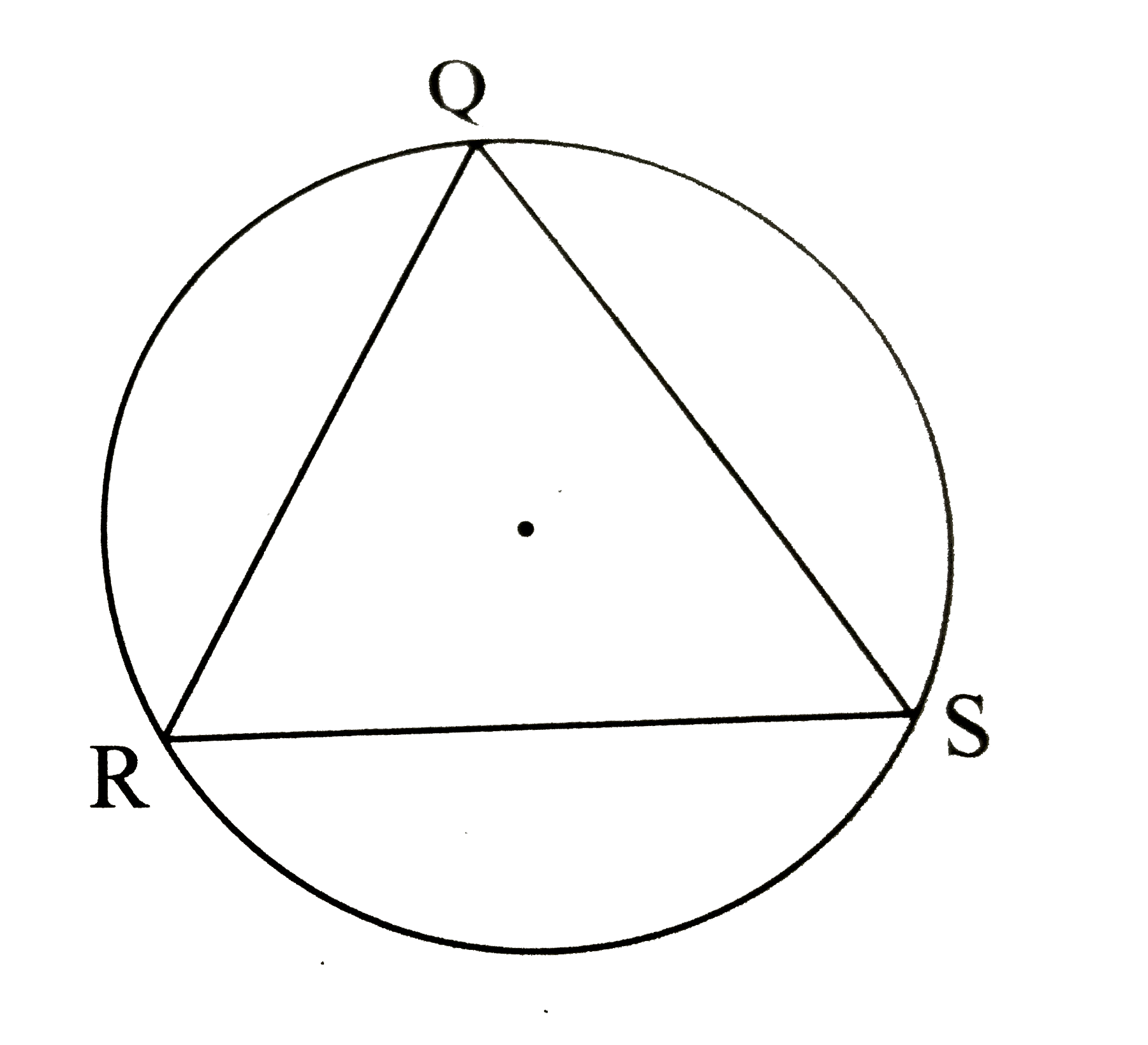
View SolutionIn the figure , ΔQRS is an equilateral triangle.
Prove that
(1) arc RS ≅arcQS≅ arc QR
(2) m (arc QRS ) =240∘.
Proof :
View SolutionIn figure, △QRS is an equilateral triangles. Prove that,
(1) arcRS≅arcQS≅arcQR
(2) m(arcQRS)=240∘.

View SolutionIn ΔPQR, if S is any point on side QR, show that PQ+QR+RP>2PS.
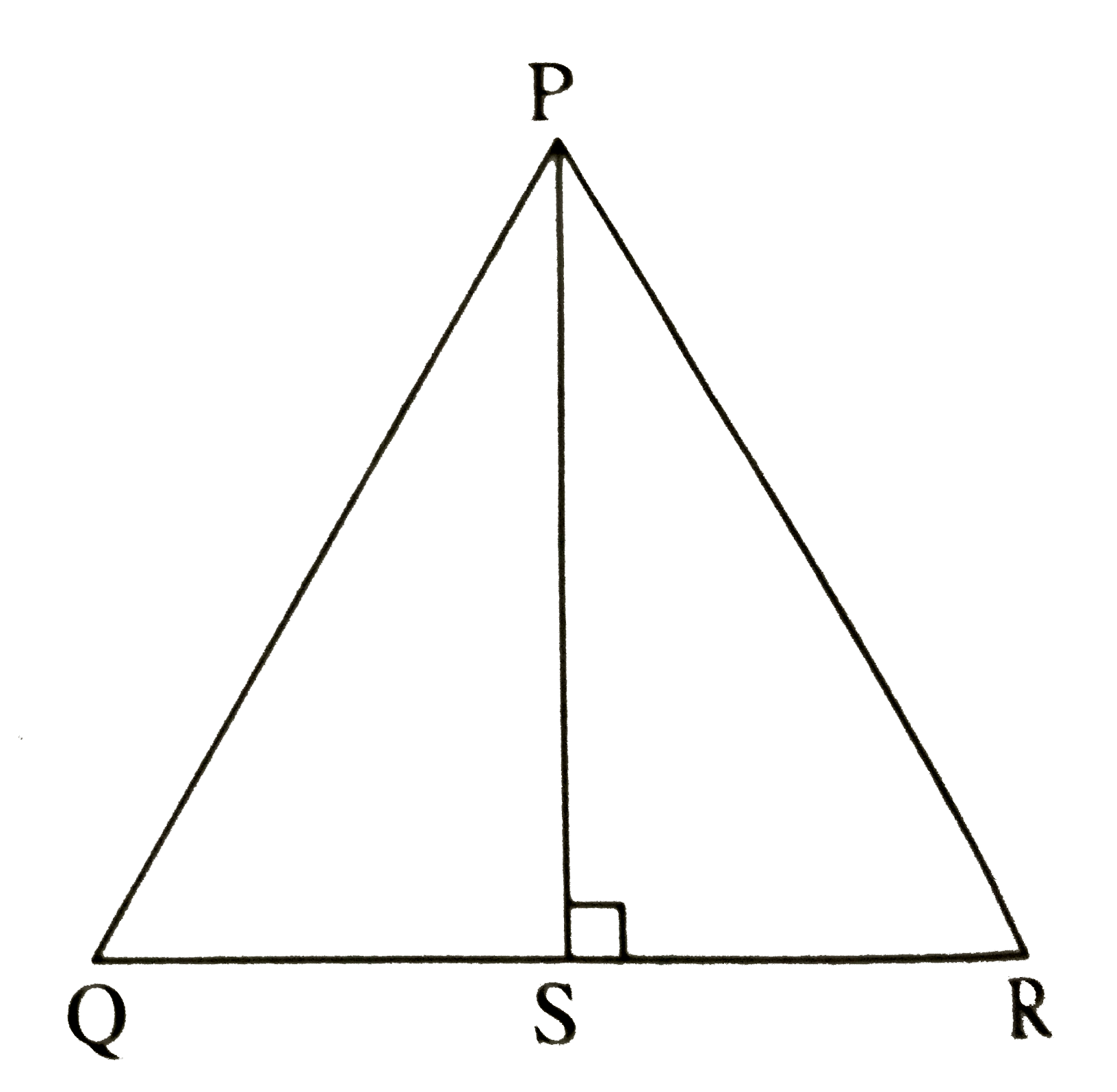
View SolutionΔPQR is an equilateral triangle. Seg PS⊥ side QR such that Q−S−R. Prove PS2=3QS2 by completing the following activity.
In ΔPQS,
∠PSQ=□……(Given)
∠Q=□………….(Angle of an equilateral triangle)
∴∠QPS=30∘.................(Remaining angle of ΔPQS)
∴ΔPQS is a □ triangle
PS=□PQ.............(Side opposite to 60∘)..............(1)
and QS=□PQ..........(Side opposite to 30∘)
PQ=2QS .....(2)
Substituting value of PQ from (2) in (1)
PS=√32×2QS
∴PS=□QS
∴PS2=3QS2......(Square both the sides)
View SolutionIn an isosceles triangle PQR, PQ =PR and S is any point on side QR. Then prove that: PQ2−PS2=QS×SR.
View SolutionIf S is a point on side PQ of a △PQR such that PS = QS = RS, then PR2+QR2 = ……………..
View SolutionIn the figure below, ΔPQR is an isosceles triangle in which ¯¯¯¯¯¯PQ=¯¯¯¯¯¯PR. PS is the bisector of ∠P. Show that
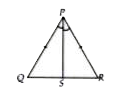
¯¯¯¯¯PS⊥¯¯¯¯¯¯QR
View Solution
