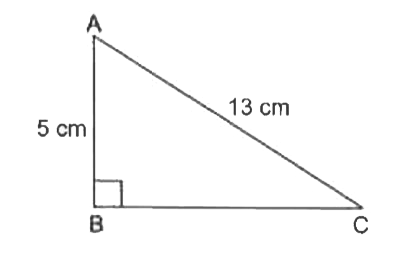
In ΔABC,∠B=90∘,BC=5cm and AC - AB = 1 cm. Find the value of sinC and cos C.
The correct Answer is:sinC=1213
cosC=513
To solve the problem step by step, we will analyze the given information and apply the Pythagorean theorem to find the values of sin C and cos C.
Step 1: Understand the triangle and given information
We have a right triangle ABC where:
- Angle B = 90°
- Side BC = 5 cm
- AC - AB = 1 cm
Step 2: Define the sides
Let:
- AB = x cm
- AC = x + 1 cm (since AC - AB = 1 cm)
Step 3: Apply the Pythagorean theorem
According to the Pythagorean theorem, in a right triangle:
AC2=AB2+BC2
Substituting the values we have:
(x+1)2=x2+52
Step 4: Expand and simplify the equation
Expanding the left side:
x2+2x+1=x2+25
Now, we can simplify this equation by subtracting x2 from both sides:
2x+1=25
Step 5: Solve for x
Now, isolate x:
2x=25−1
2x=24
x=12
Step 6: Find the lengths of AB and AC
Now that we have x:
- AB = x = 12 cm
- AC = x + 1 = 12 + 1 = 13 cm
Step 7: Calculate sin C
The sine of angle C is given by the ratio of the opposite side (AB) to the hypotenuse (AC):
sinC=ABAC=1213
Step 8: Calculate cos C
The cosine of angle C is given by the ratio of the adjacent side (BC) to the hypotenuse (AC):
cosC=BCAC=513
Final Answers
- sinC=1213
- cosC=513
---
We have a right triangle ABC where:
- Angle B = 90°
- Side BC = 5 cm
- AC - AB = 1 cm
Let:
- AB = x cm
- AC = x + 1 cm (since AC - AB = 1 cm)
According to the Pythagorean theorem, in a right triangle:
AC2=AB2+BC2
Substituting the values we have:
(x+1)2=x2+52
Expanding the left side:
x2+2x+1=x2+25
Now, we can simplify this equation by subtracting x2 from both sides:
2x+1=25
Now, isolate x:
2x=25−1
2x=24
x=12
Now that we have x:
- AB = x = 12 cm
- AC = x + 1 = 12 + 1 = 13 cm
The sine of angle C is given by the ratio of the opposite side (AB) to the hypotenuse (AC):
sinC=ABAC=1213
The cosine of angle C is given by the ratio of the adjacent side (BC) to the hypotenuse (AC):
cosC=BCAC=513
- sinC=1213
- cosC=513
Topper's Solved these Questions
- PRACTICE TEST-1 Book:CBSE COMPLEMENTARY MATERIALChapter:PRACTICE TEST-1 Exercise:SECTION-B
Explore 7 Videos
- PRACTICE PAPER- I (WITH SOLUTIONS) CLASS: X Mathematics (Standard)Book:CBSE COMPLEMENTARY MATERIALChapter:PRACTICE PAPER- I (WITH SOLUTIONS) CLASS: X Mathematics (Standard)Exercise:SECTION -D
Explore 6 Videos
- PRACTICE TEST-IIBook:CBSE COMPLEMENTARY MATERIALChapter:PRACTICE TEST-IIExercise:Section C
Explore 14 Videos
Similar Questions
Knowledge Check
In △ABC, ∠B=90∘ , AB=5cm and AC=13cm. Then, BC = ?
 A8 cmB18 cmC12 cmDnone of these
A8 cmB18 cmC12 cmDnone of theseIn ΔABC,∠B=90∘,AC=29cmandBC=20cm. Then 1−sinA+cosA1+sinA+cosA is equal to :
AA)38BB)37CC)12DD)14In Δ ABC, AB = 6 cms, BC = 10 cms, AC = 8cm and ADI_BC. Find the value of the ratio of BD:DC.
A3:4B9:16C4:5D16:25
In triangle ABC, ∠B=90∘, AC+BC=25 and AB=5, determine the value of sinA, cosA and tanA
View SolutionIn a ΔABC,∠A=120∘,AB=6cm,AC=8cm find the l,ength of side BC.
View SolutionIn the given figure,ABC in a right-angled triangle,right-angled atB.IfBC=5cmandAC-AB=1cm,f∈dthevalueofcosecAandcos A
View SolutionIn ΔABC,right -angled at B,AB=5cmandBC=12cm. find the values of sinA,secA,sinCandsecC.
View SolutionIn a ΔABC,AB=10cm,BC=12andAC=18 cm. Find the length of smallest altitude.
View Solution