In ΔABC, E is mid-point of side AB and EBCD is a parallelogram. If the area of ΔABC is 80 cm, find the area of parallelogram EBCD.
The correct Answer is:80cm2
To solve the problem, we need to find the area of parallelogram EBCD given that the area of triangle ABC is 80 cm² and E is the midpoint of side AB.
1. Identify the Midpoint:
Since E is the midpoint of side AB, we can denote the lengths as follows:
AE=EB=AB2
2. Use the Area Formula for Triangle ABC:
The area of triangle ABC can be calculated using the formula:
Area=12×base×height
Here, we can take AB as the base and EC as the height from point C to line AB. Therefore:
Area of △ABC=12×AB×EC
3. Express Area in Terms of EB and EC:
Since E is the midpoint, we can express AB as:
AB=2×EB
Substituting this into the area formula gives:
Area of △ABC=12×(2×EB)×EC=EB×EC
4. Set Up the Equation:
We know from the problem that the area of triangle ABC is 80 cm². Therefore:
EB×EC=80 cm2
5. Calculate the Area of Parallelogram EBCD:
The area of parallelogram EBCD can be calculated using the base EB and height EC:
Area of parallelogram EBCD=base×height=EB×EC
Since we established that EB×EC=80 cm2, we find that:
Area of parallelogram EBCD=80 cm2
Final Answer:
The area of parallelogram EBCD is 80 cm².
---
Since E is the midpoint of side AB, we can denote the lengths as follows:
AE=EB=AB2
The area of triangle ABC can be calculated using the formula:
Area=12×base×height
Here, we can take AB as the base and EC as the height from point C to line AB. Therefore:
Area of △ABC=12×AB×EC
Since E is the midpoint, we can express AB as:
AB=2×EB
Substituting this into the area formula gives:
Area of △ABC=12×(2×EB)×EC=EB×EC
We know from the problem that the area of triangle ABC is 80 cm². Therefore:
EB×EC=80 cm2
The area of parallelogram EBCD can be calculated using the base EB and height EC:
Area of parallelogram EBCD=base×height=EB×EC
Since we established that EB×EC=80 cm2, we find that:
Area of parallelogram EBCD=80 cm2
The area of parallelogram EBCD is 80 cm².
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - CIRCLE
7 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - STATISTICS
5 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - CONSTRUCTIONS OF POLYGONS
4 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Graphical solution
10 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)
12 Videos
Similar Questions
ABCD is a parallelogram. Find the ratio of the area of Δ ABC to the area of the parallelogram ABCD.
View SolutionIn a ΔABC,D,EandF are the mid-point of sides BC, CA and AB respectively. If area of ΔABC=16cm2, find the area of trapezium FBCE
View SolutionE, F, G and H are the mid-points of the sides of a parallelogram ABCD. Show that area of quadrilateral EFGH is half of the area of parallelogram ABCD.
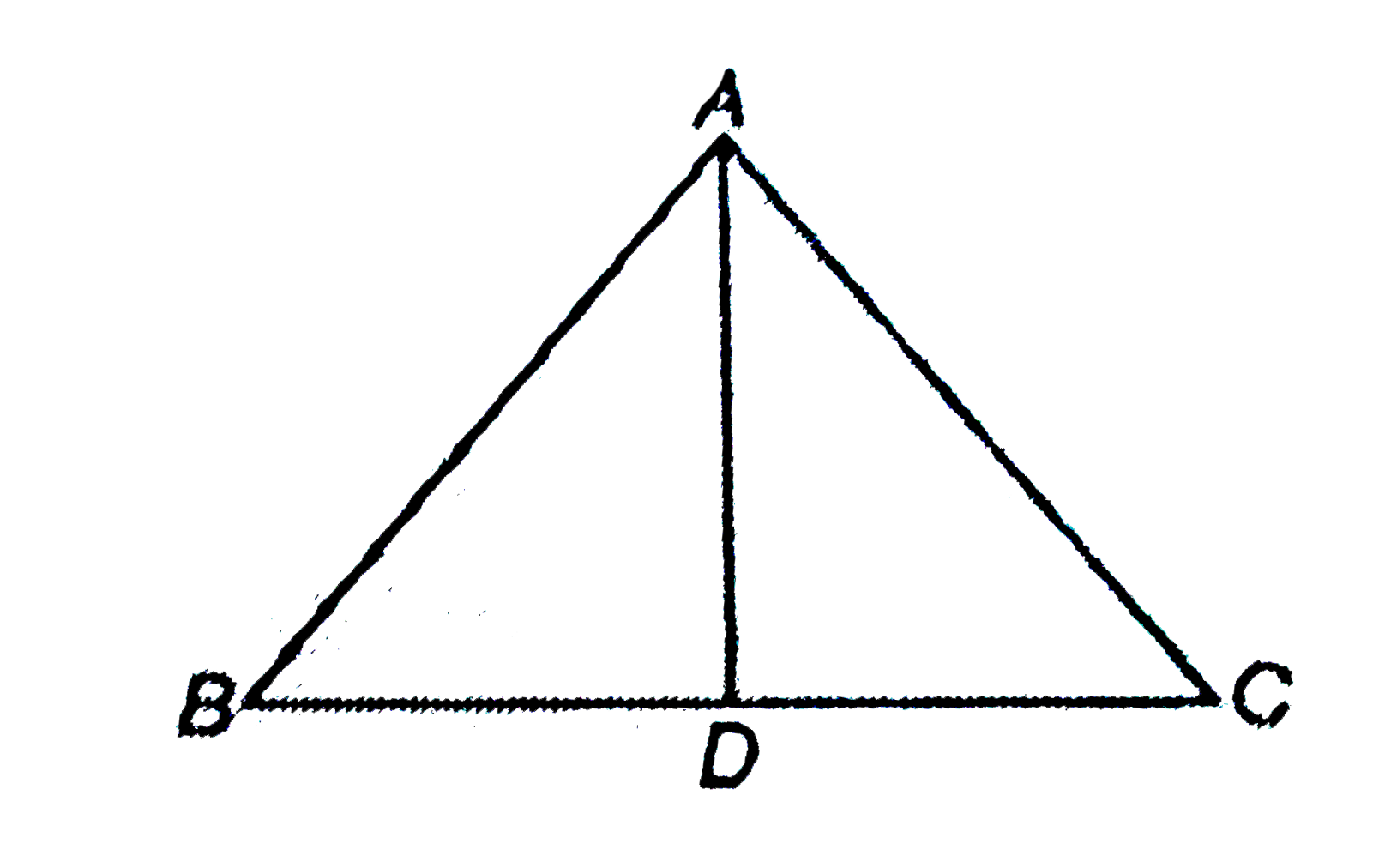
View SolutionIn the given figure AD is the median. If the area of ΔABD=10cm2, find the area of ΔABC
View SolutionABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively.
Prove that area of triangle APQ= 18 of the area of parallelogram ABCD.
View SolutionABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively.
Prove that area of triangle APQ= 18 of the area of parallelogram ABCD.
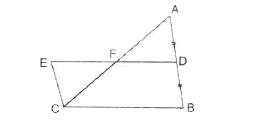
View SolutionIn the given figure, D is mid-point of side AB of △ABC and BDEC is a parallelogram.
Prove that :
Area of ΔABC = Area of //gmBDEC
View SolutionE is the mid-point of side AB and F is the mid point of side DC of parallelogram ABCD . Prove that AEFD is a parallelogram.
View SolutionIn triangle ABC,D is the midpoint of AB, E is the midpoint of DB and F is the midpoint of BC. If the area of ΔABC is 96, the area of ΔAEF is
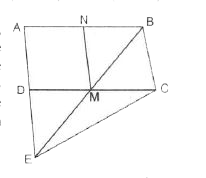
View SolutionIn the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD.
If the area of parallelogram ABCD is 48cm2,
(i) State the area of the triangle BEC.
(ii) name the parallelofram which is equal in area to the triangle BEC.
View Solution
