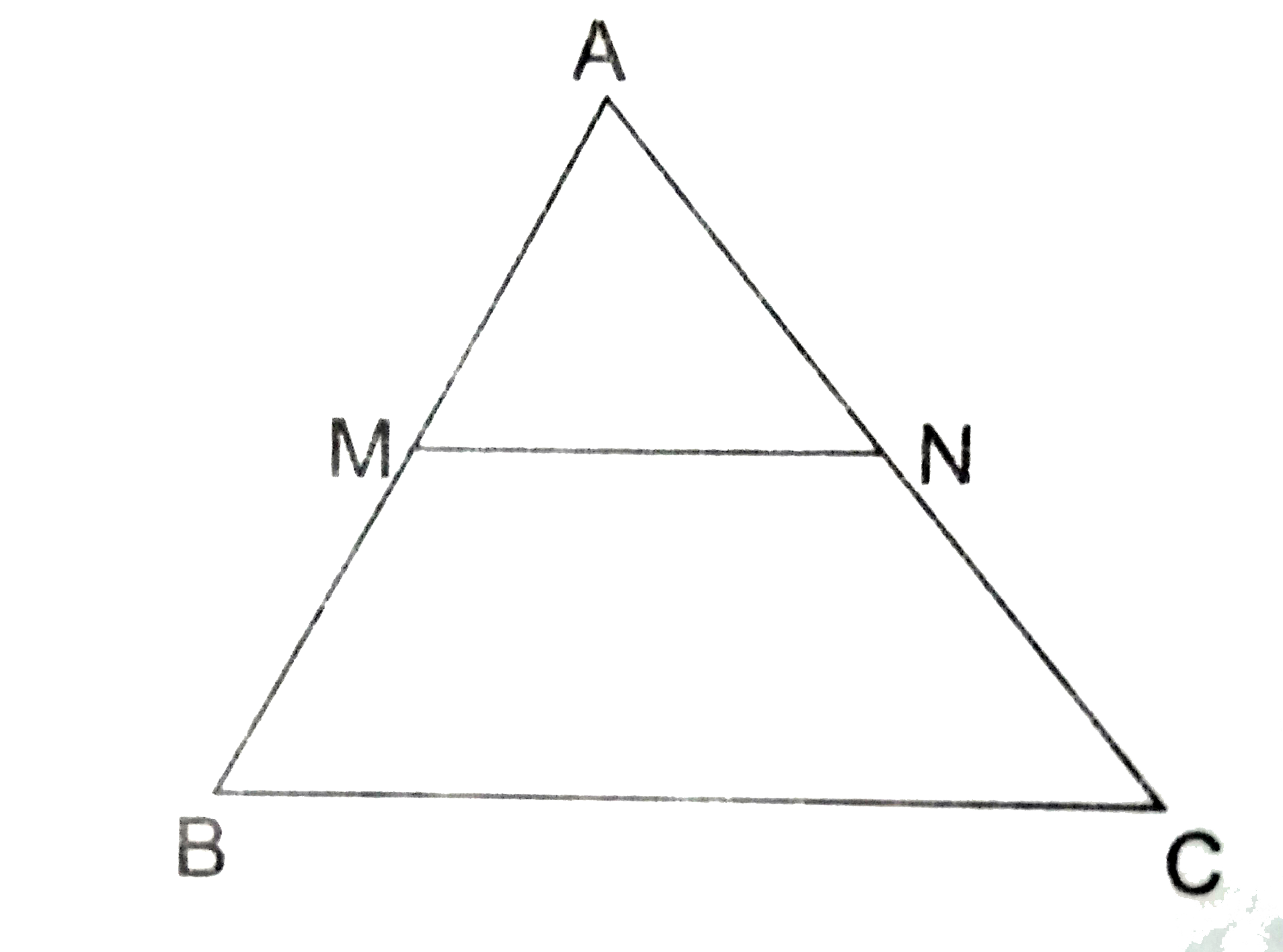
In ΔABC,MandN are points on the sides AB and AC respectively such that BM=CN. If ∠A=∠C then show that MN∣∣BC.
∠B=∠C⇒AB=AC⇒AM+BM=AN+CN⇒AM=AN[∴BM=CM]
Now, AM=AN,BM=CN⇒AMBM=ANCN
⇒AMMB=ANNC⇒MN∣∣BC.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7B19videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7C13videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A1videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 1127videos
T-RATIOS OF SOME PARTICULAR ANGLES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself20videos
TRIGONOMETRIC IDENTITIES
Similar Questions
Knowledge Check
- Question 1 - Select One
In right angled ΔABC,∠B=90∘, if P and Q are points on the sides AB and BC respectively, then :
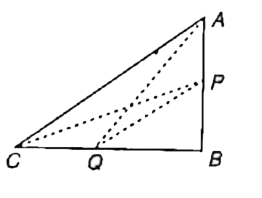 AAQ2+CP2=2(AC2+PQ2)BAQ2+CP2=AC2+PQ2C(AQ2+CP2)=12(AC2+PQ2)D(AQ+CP)=12(AC+PQ)
AAQ2+CP2=2(AC2+PQ2)BAQ2+CP2=AC2+PQ2C(AQ2+CP2)=12(AC2+PQ2)D(AQ+CP)=12(AC+PQ) - Question 2 - Select One
P is any point on the side BC of a △ABC. P is joined to a. If D and E are the midpoints of the sides AB and AC respectively and M and N are the midpoints of BP and CP respectively then quadrilateral DENM is
Aa trapeziumBa parallelogramCa rectangleDa rhombus - Question 3 - Select One
In ΔABC, AB=AC and D is a point on side AC such that BD = BC, If AB = 12.5 cm and BC = 5 cm, then what is the measure of DC ?
A2 cmB2.5 cmC3 cmD1.8 cm
ΔABC lies in the plane with A(0,0),B(0,1) and C(1.0). Points M and N are chosen on AB and AC, respectively, such that MN is parallel to BC and MN divides the area of ΔABC in half. Find the coordinates of M.
View SolutionLet ABC be a triangle. Three points D, E and F are on the sides AB, AC and BC respectively so that BDEF is a parallelogram. M and N are mid points of the sides DE and EF. If vector ¯¯¯¯¯¯¯¯MN=14¯¯¯¯¯¯AC. Then find the ratio in which D and F divides the sides AB and BC.
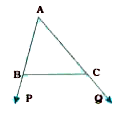
View SolutionIn the given figure, sides AB and AC of △ ABC are extended to points P and Q respectively. Also, ∠PBC<∠QCB. Show that AC > AB
 View Solution
View SolutionIf DandE are the mid-points of sides ABandAC of a triangle ABC respectively, show that →BE+→DC=32→BC.
View SolutionD is a point on side BC of ΔABC such that AD=AC. Show that AB>AD.
View Solution

