In ΔPQR , right - angled at Q , PR +QR = 25 cm and PQ = 5cm . Determine the values of sin P , cos P and tan P.
To solve the problem, we will follow these steps:
Step 1: Understand the triangle and given information
We have a right triangle ΔPQR with the right angle at Q. We are given:
- PQ=5 cm
- PR+QR=25 cm
Step 2: Assign variables
Let:
- PR=x cm
- QR=25−x cm (from the equation PR+QR=25)
Step 3: Apply the Pythagorean theorem
According to the Pythagorean theorem:
PR2=PQ2+QR2
Substituting the known values:
x2=52+(25−x)2
Step 4: Expand the equation
Expanding the equation:
x2=25+(25−x)(25−x)
x2=25+(625−50x+x2)
x2=25+625−50x+x2
Step 5: Simplify the equation
Cancel x2 from both sides:
0=650−50x
Step 6: Solve for x
Rearranging gives:
50x=650
x=65050=13 cm
So, PR=13 cm.
Step 7: Calculate QR
Now, substitute x back to find QR:
QR=25−PR=25−13=12 cm
Step 8: Calculate sinP, cosP, and tanP
Using the definitions of trigonometric ratios:
- tanP=QRPQ=125
- sinP=QRPR=1213
- cosP=PQPR=513
Final Values
Thus, the values are:
- tanP=125
- sinP=1213
- cosP=513
---
- PQ=5 cm
- PR+QR=25 cm
- PR=x cm
- QR=25−x cm (from the equation PR+QR=25)
PR2=PQ2+QR2
Substituting the known values:
x2=52+(25−x)2
x2=25+(25−x)(25−x)
x2=25+(625−50x+x2)
x2=25+625−50x+x2
0=650−50x
50x=650
x=65050=13 cm
QR=25−PR=25−13=12 cm
- tanP=QRPQ=125
- sinP=QRPR=1213
- cosP=PQPR=513
- tanP=125
- sinP=1213
- cosP=513
Topper's Solved these Questions
- INTRODUCTION TO TRIGONOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Problems From NCERT/exemplar
29 Videos
- INTRODUCTION TO TRIGONOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Exercise 8a
20 Videos
- CONSTRUCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 11 B
10 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Revision Exercise Long Answer Questions
8 Videos
Similar Questions
In ΔPQR,right angled at Q, PR+QR=25cm and PQ=5cm. Determine the values of sinP,cosP and tanP.
View SolutionIn ΔPQR,right angled at Q, PR+QR=25cm and PQ=5cm. Determine the values of sinP,cosP and tanP.
View SolutionIn DelatOPQ , right - angled at P , OP = 7 cm and OQ - PQ =1 cm . Determine the values of sinQ and cos Q .
View SolutionIn PQR , right-angled at Q, PQ=3cm and PR=6cm . Determine ∠P and ∠R .
View SolutionIn ΔOPQ, right-angled at P, OP = 7 cm andOQ − PQ = 1 cmDetermine the values of sin Q and cos Q.
View SolutionIn △PQR , right-angled at Q, PQ=3cm and PR=6cm . Determine ∠P and ∠R .
View SolutionIn △OPQ right angled at P, OP=7cm , OQ−PQ=1cm . Determine the values of sinQ and cosQ .
View SolutionIn a △ABC , right angled at B , AB=24cm, BC=7cm . DeterminesinC,cosC
View SolutionIn ΔPQR, If angleR=angleP, QR=4 cm and PR = 5 cm. Then, the length of PQ is
View SolutionIn the right-angled triangle QPR, PM altitude.
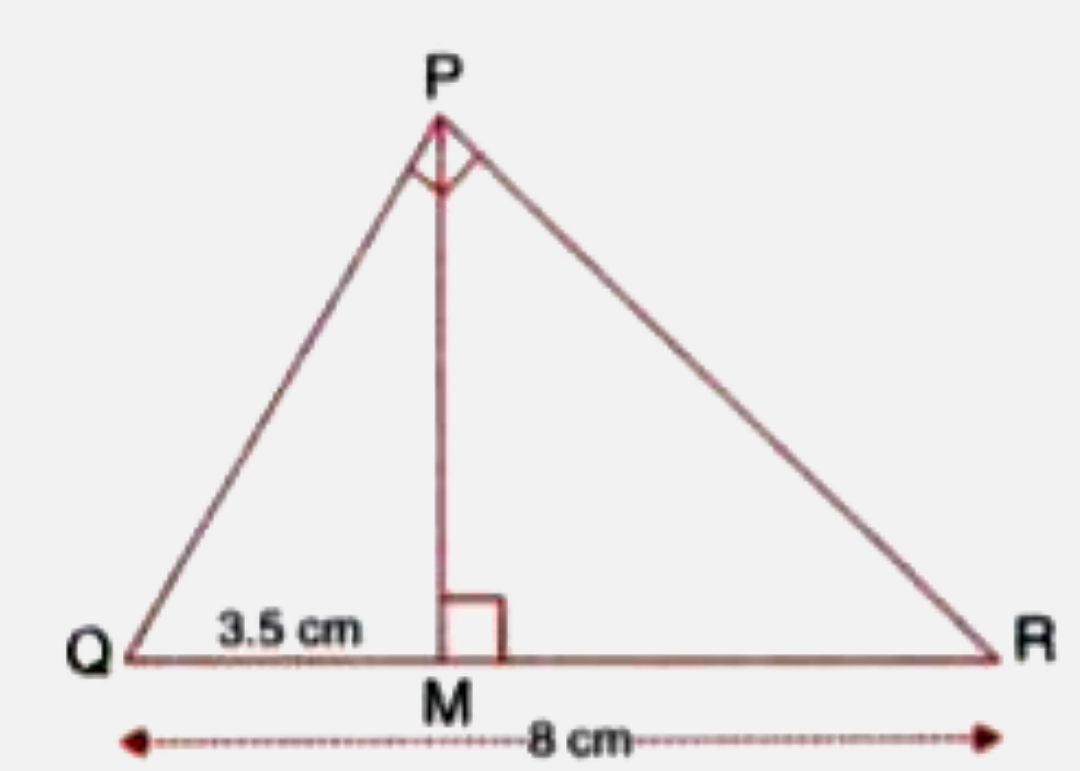
Given that QR = 8 cm and MQ = 3-5 cm, calculate the value of PR.
View Solution
