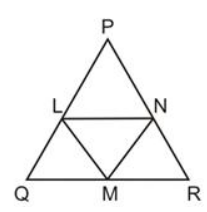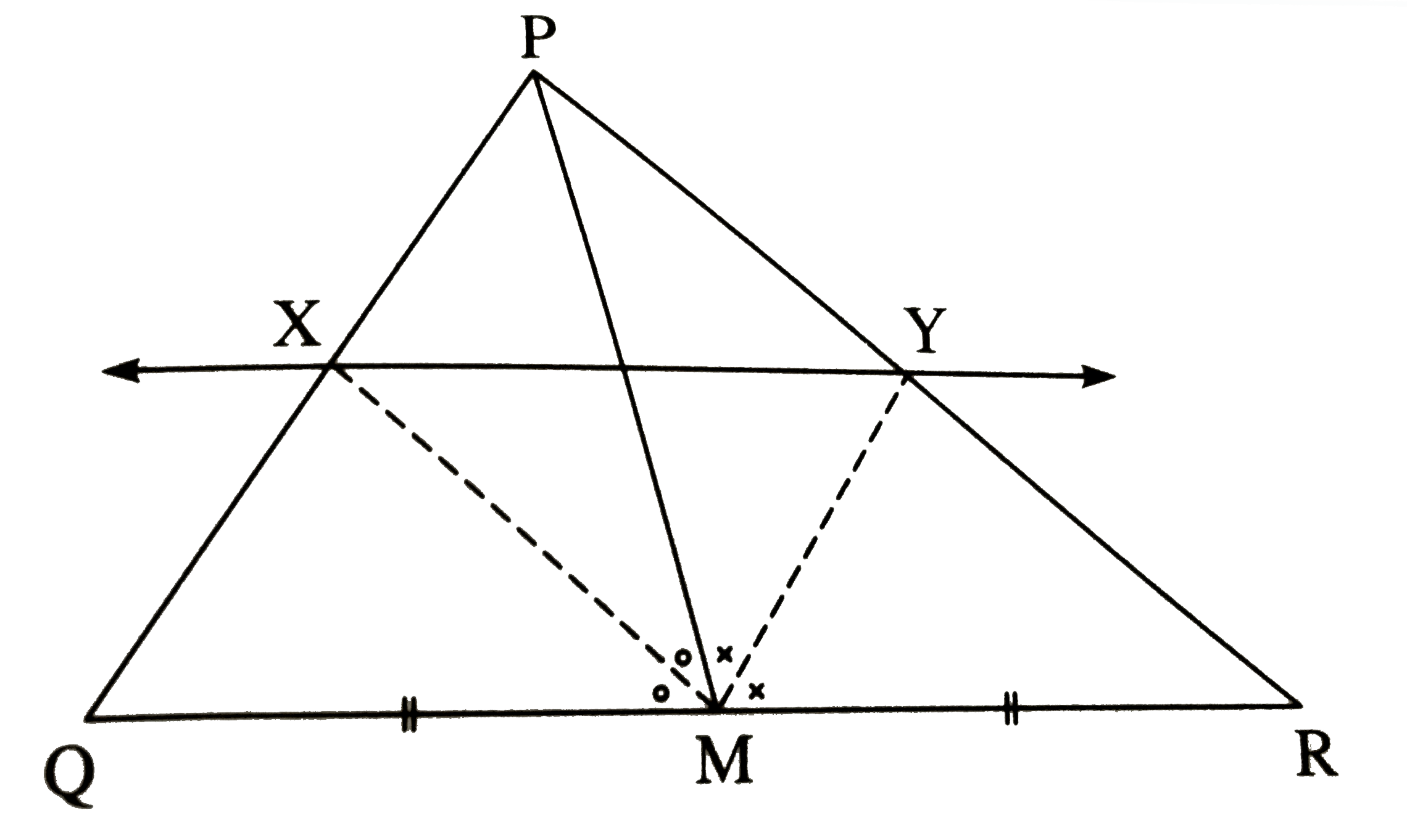
In ΔPQR seg PM is a median. Angle bisectors of ∠PMQ and ∠PMR interesect side PQ and side PR in points X and Y respectively. Prove that XY∣∣QR.
Complete the proof byfilling in the boxes:
The correct Answer is:∴XY||QR
Step by step video & image solution for In DeltaPQR seg PM is a median. Angle bisectors of /_PMQ and /_PMR interesect side PQ and side PR in points X and Y respectively. Prove that XY||QR. Complete the proof byfilling in the boxes: by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Activites for Practice4videos
SIMILARITY
- BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Multiple Choice Questions28videos
SIMILARITY
- BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Practice Set 1.47videos
SIMILARITY
- BOOK - TARGET PUBLICATIONCHAPTER - QUESTION FROM STD. IXEXERCISE - Statistics14videos
QUESTION FROM STD. IX
- BOOK - TARGET PUBLICATIONCHAPTER - STATISTICSEXERCISE - Problem Set-621videos
STATISTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
A circle passing through points Q and R of triangle PQR, cut the sides PQ and PR at point X and Y respectively. If PQ = PR, then what is the value (in degrees) of ∠PRQ+∠QXY ?
A120B150C240D180 - Question 2 - Select One
In ΔPQR, a line parallel to side QR cuts the side PQ and PR at points M and N respectively and point M divide PQ in the ratio of 1 : 2. If area of ΔPQR is 360 cm2, then what is the area (in cm2) of quadrilateral MNRQ?
A160B320C120D96
Seg PM is a median of ΔPQR. If PQ=40,PR=42 and PM =29, find QR.
View SolutionIn ΔPQR side QR is extended to S and angle bisector of ∠PQRand∠PRS meets at point T. If ∠QPR=80∘ find ∠QTR.
View SolutionIn ΔPQR, seg PM is median. PM=9, PQ2+PR2=290 then find length of seg QR.
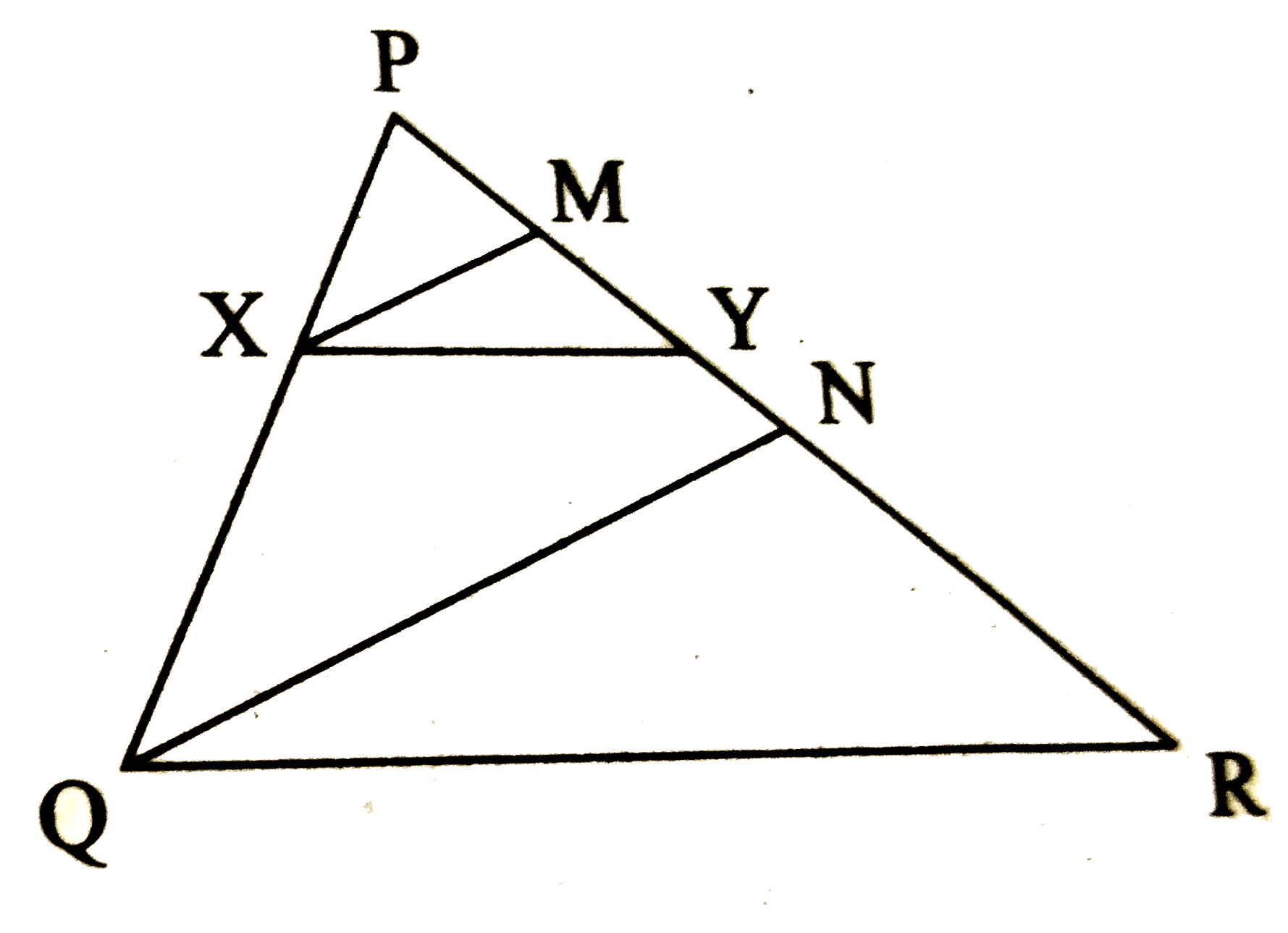
View SolutionIn ΔPQR, seg XY∣∣ side QR. M and N are the midpoints of seg PY and side PR respectively, P−M−Y−N−R.
Prove that (i)ΔPXM~ΔPQN
(ii) seg XM∣∣ seg QN.
 View Solution
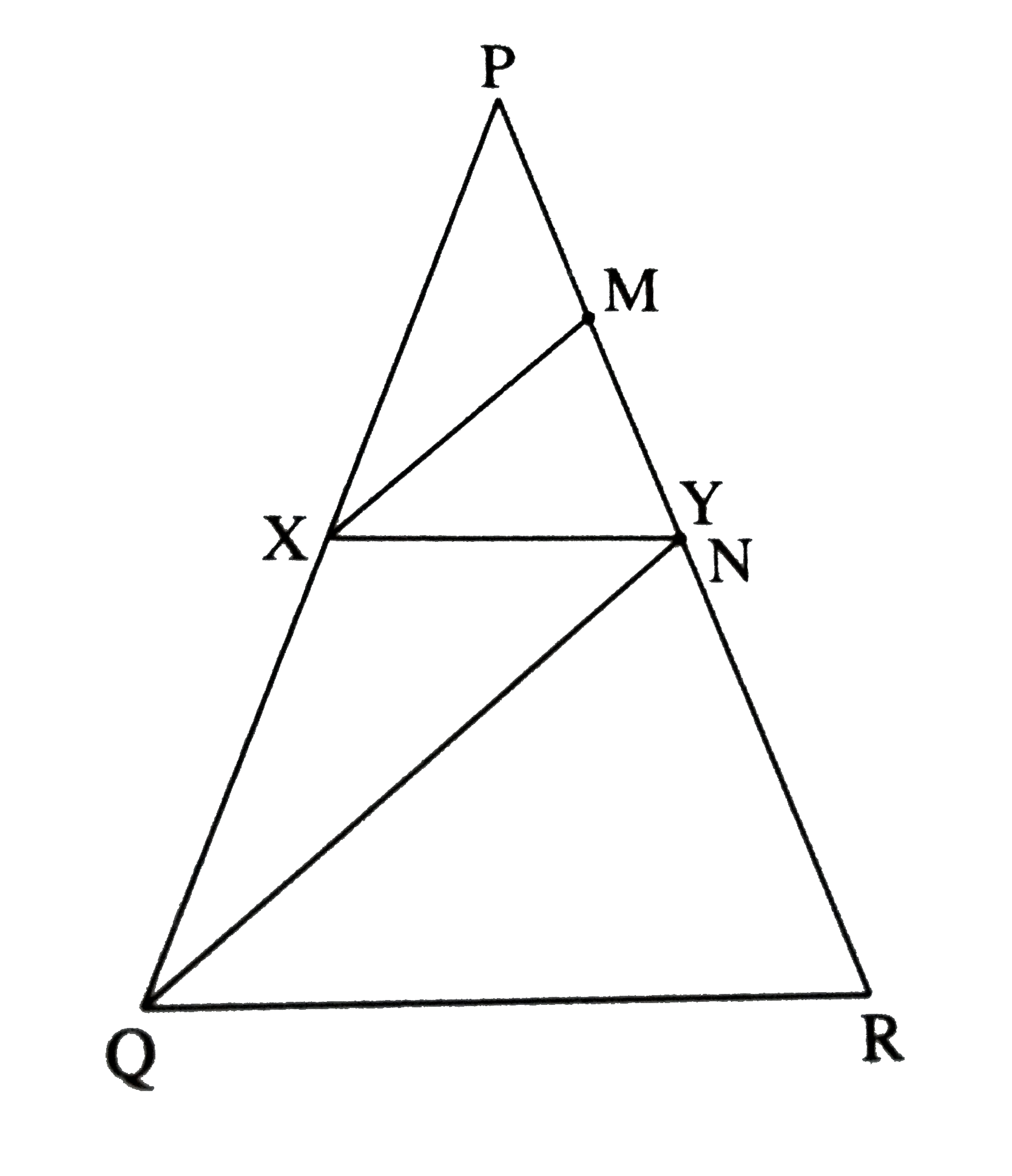
View SolutionIn ΔPQR, set XY∣∣ sides QR, M and N are midpoints of seg PY and seg PR respectively. Prove that:
(i) ΔPXM~ΔPQN (ii) segXM∣∣secQN.
 View Solution
View SolutionThe sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and the median PM of triangle PQR respectively. Prove that the triangles ABC and PQR are congruent.
View Solution