In ΔPQR side QR is extended to S and angle bisector of ∠PQRand∠PRS meets at point T. If ∠QPR=80∘ find ∠QTR.
30∘
40∘
60∘
80∘
To solve the problem, we need to find the angle ∠QTR in triangle PQR where side QR is extended to point S and the angle bisector of ∠PQR and ∠PRS meets at point T. We are given that ∠QPR=80∘.
1. Draw the Triangle and Extend Side QR:
- Draw triangle PQR with points P,Q,R.
- Extend side QR to point S.
2. Identify the Angles:
- Mark ∠QPR=80∘.
- Let ∠PQR=x and ∠PRS=y.
3. Use the Angle Bisector Theorem:
- Since T is the intersection of the angle bisectors of ∠PQR and ∠PRS, we can denote:
- Let ∠QPT=∠PQR/2=x/2.
- Let ∠RPT=∠PRS/2=y/2.
4. Apply the Exterior Angle Theorem:
- In triangle PQR, the exterior angle ∠PRS can be expressed as:
y=∠QPR+∠PQR=80∘+x
5. Set Up the Equations:
- From the angle bisector properties:
∠QPR+2⋅x2=2⋅y2
- This simplifies to:
80∘+x=y
6. Substitute for y:
- Substitute y in terms of x:
y=80∘+x
7. Find the Relationship:
- In triangle QTR, we can express ∠QTR as:
∠QTR+x2=y2
- Substitute y:
∠QTR+x2=80∘+x2
8. Rearranging the Equation:
- Rearranging gives:
2⋅∠QTR+x=80∘+x
- Cancel x from both sides:
2⋅∠QTR=80∘
9. Solve for ∠QTR:
- Divide by 2:
∠QTR=80∘2=40∘
Final Answer:
Thus, the measure of ∠QTR is 40∘.
- Draw triangle PQR with points P,Q,R.
- Extend side QR to point S.
- Mark ∠QPR=80∘.
- Let ∠PQR=x and ∠PRS=y.
- Since T is the intersection of the angle bisectors of ∠PQR and ∠PRS, we can denote:
- Let ∠QPT=∠PQR/2=x/2.
- Let ∠RPT=∠PRS/2=y/2.
- In triangle PQR, the exterior angle ∠PRS can be expressed as:
y=∠QPR+∠PQR=80∘+x
- From the angle bisector properties:
∠QPR+2⋅x2=2⋅y2
- This simplifies to:
80∘+x=y
- Substitute y in terms of x:
y=80∘+x
- In triangle QTR, we can express ∠QTR as:
∠QTR+x2=y2
- Substitute y:
∠QTR+x2=80∘+x2
- Rearranging gives:
2⋅∠QTR+x=80∘+x
- Cancel x from both sides:
2⋅∠QTR=80∘
- Divide by 2:
∠QTR=80∘2=40∘
Thus, the measure of ∠QTR is 40∘.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a ΔABC, the internal angle bisector of ∠ABC and ∠ACB meets at point ‘O’. If the ∠BOC is 134∘, then find ∠BAC.
Aa) 76∘Bb) 84∘Cc) 92∘Dd) 88∘In triangle PQR, the sides PQ and PR are produced to A and B respectively. The bisectors of ∠AQR and ∠BRQ intersect at point O. If ∠QOR=50∘, what is the value (in degree) of ∠QPR?
A1) 50B2) 60C3) 80D4)100In a ΔPQR, the sides PQ and PR and are produced to S and T respectively. Bisectors of ∠SQRand∠QRT meet at the point O. If ∠P=66∘, then what is the value of ∠QOR?
A47∘B50∘C57∘D67∘
In △PQR , sides PQ and PR are extended to S and T respectively . OQ and OR are bisector of ∠RQS and ∠QRT meeting at O. Show that 2∠QOR=∠PQR+∠QRP
View SolutionThe sides PQ and PR of △PQR are produced to points S and T, respectively. The bisectors of ∠SQR and ∠TRQ meet at U. If ∠QUR=79∘ , then the measure of ∠P is:
त्रिभुज PQR की भुजाओ PQ और QR को क्रमशः S और T तक बढ़ाया जाता है| ∠SQR और ∠TRQ के समद्विभाजक U पर मिलते हैं| यदि ∠QUR=79∘ है, तो कोण P का मान ज्ञात करें |
View SolutionΔABC ,angle B external angle C meets at P ∠A=80 then ∠BPC = ?
View SolutionIn ΔPQR, PS and PT are bisectors of ∠QPRand∠QPS respectively. If ∠QPT=30∘,PT=9cmandTR=15cm, then what is the area (in cm2) of ΔPTR?
View SolutionIn the adjacent figure, the bisectors of ∠Aand∠B meet in a point P. If ∠C=100∘and∠D=60∘, find the measure of ∠APB.
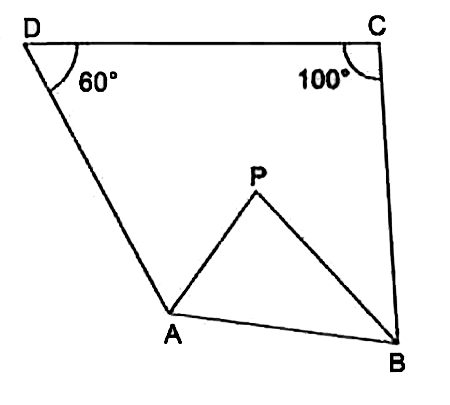
View Solution
