In Fig. 10.61, is a tangent to the given circle at point such that and . The other tangents and are drawn respectively from and to the circle and meet when produced at making a right angle triangle. Calculate (i) (ii) radius of the circle. (FIGURE)
To solve the problem step by step, we will follow the instructions provided in the video transcript and apply the necessary mathematical concepts.
1. Identify Given Information:
- Length of tangent BD=30cm
- Length of tangent CD=7cm
- Triangle BAC is a right triangle with ∠BAC=90∘.
2. Understand the Geometry:
- Since BD and CD are tangents to the circle from points B and C, we know that:
- BE=BD=30cm (tangent from B)
- CF=CD=7cm (tangent from C)
3. Apply Pythagorean Theorem:
- In triangle BAC, we can apply the Pythagorean theorem:
AB2+AC2=BC2
- Here, AB=BE+AE=30+R and AC=CF+AF=7+R.
- The hypotenuse BC=BD+CD=30+7=37cm.
4. Set Up the Equation:
- Substitute the lengths into the Pythagorean theorem:
(30+R)2+(7+R)2=372
5. Expand the Equation:
- Expanding both sides:
(30+R)2=900+60R+R2
(7+R)2=49+14R+R2
372=1369
- Combine these into one equation:
900+60R+R2+49+14R+R2=1369
- Simplifying gives:
2R2+74R+949=1369
6. Rearrange the Equation:
- Rearranging leads to:
2R2+74R−420=0
- Divide the entire equation by 2:
R2+37R−210=0
7. Use the Quadratic Formula:
- Apply the quadratic formula R=−b±√b2−4ac2a:
R=−37±√372−4⋅1⋅(−210)2⋅1
- Calculate the discriminant:
372=1369and4⋅210=840
√1369+840=√2209=47
- Substitute back into the formula:
R=−37±472
8. Calculate the Two Possible Values for R:
- Calculate the two potential solutions:
R=102=5(valid, since radius cannot be negative)
R=−842=−42(not valid)
9. Final Answers:
- The radius of the circle R=5cm.
- The length AF=R=5cm.
Summary of Answers:
- (i) AF=5cm
- (ii) Radius of the circle =5cm
- Length of tangent BD=30cm
- Length of tangent CD=7cm
- Triangle BAC is a right triangle with ∠BAC=90∘.
- Since BD and CD are tangents to the circle from points B and C, we know that:
- BE=BD=30cm (tangent from B)
- CF=CD=7cm (tangent from C)
- In triangle BAC, we can apply the Pythagorean theorem:
AB2+AC2=BC2
- Here, AB=BE+AE=30+R and AC=CF+AF=7+R.
- The hypotenuse BC=BD+CD=30+7=37cm.
- Substitute the lengths into the Pythagorean theorem:
(30+R)2+(7+R)2=372
- Expanding both sides:
(30+R)2=900+60R+R2
(7+R)2=49+14R+R2
372=1369
- Combine these into one equation:
900+60R+R2+49+14R+R2=1369
- Simplifying gives:
2R2+74R+949=1369
- Rearranging leads to:
2R2+74R−420=0
- Divide the entire equation by 2:
R2+37R−210=0
- Apply the quadratic formula R=−b±√b2−4ac2a:
R=−37±√372−4⋅1⋅(−210)2⋅1
- Calculate the discriminant:
372=1369and4⋅210=840
√1369+840=√2209=47
- Substitute back into the formula:
R=−37±472
- Calculate the two potential solutions:
R=102=5(valid, since radius cannot be negative)
R=−842=−42(not valid)
- The radius of the circle R=5cm.
- The length AF=R=5cm.
- (i) AF=5cm
- (ii) Radius of the circle =5cm
Topper's Solved these Questions
Similar Questions
AB and CD are two chords of a circle such that AB=6 cm, CD=12 cm and ABCD. If the distance between AB and CD is 3 cm, find the radius of the circle.
View SolutionAB and CD are two chords of a circle such that AB = 6 cm, CD = 12 cm and AB || CD. If the distance between AB and CD is 3 cm, find the radius of the circle
View SolutionIn Fig 31, ABCD is a rectangle with dimensions 32 m by 18 m. ADE is a triangle such that EF⊥AD and EF=14 cm. Calculate the area of the shaded region.
View SolutionLet C1andC2 be externally tangent circles with radius 2 and 3 respectively. Let C1andC2 both touch circle C3 internally at point A and B respectively. The tangents to C3 at A and B meet at T and TA = 4, then radius of circle C3 is :
View SolutionIf A, B, C and D are four points such that ∠BAC=30∘and∠BDC=60∘,then D is the centre of the circle through A, B and C.
View SolutionIf triangle ABC is similar to triangle DEF such that BC=3CM,EF=4cm and area of triangle ABC=54cm2 . Determine the area of triangle DEF.
View SolutionAs shown in the figure, circles with centres A.B and C are externally tangent to each other and internally tangent to the circle with centre D Circles B and C are congruent. Circle A has radius 1 and passes through D. The radius of the circle B, is
View SolutionIn the given circle in Figure-1 , number of tangents parallel to tangent PQ is
(A) 0
(B) many
(C) 2
(D) 1
View SolutionAB is a diameter of a circle. CD is a.chord parallel to AB and 2CD=AB. The tangent at B meets the line AC produced at E and AE=K.AB, then K is equal to
View SolutionIf the diagram, DC is a diameter of the large circle centered at A, and AC is a diameter of the smaller circle centered at B. If DE is tangent to the smaller circle at F and DC=12 then the length of DE is
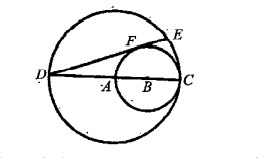 .
.
View Solution
