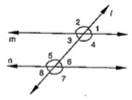
In Fig. 49, m∣∣n and ∠1=650. Find ∠5 and ∠8.
To solve the problem, we need to find the values of angles 5 and 8 given that lines m and n are parallel and angle 1 is 65 degrees.
1. Identify the relationship between angles: Since lines m and n are parallel, angle 1 and angle 2 form a linear pair. Therefore, their sum is 180 degrees.
Angle 1+Angle 2=180∘
2. Substitute the known value of angle 1: We know that angle 1 = 65 degrees. Substitute this value into the equation.
65∘+Angle 2=180∘
3. Solve for angle 2: Rearranging the equation gives us:
Angle 2=180∘−65∘=115∘
4. Use the property of corresponding angles: Angle 2 corresponds to angle 5 because they are on the same side of the transversal and between the two parallel lines. Therefore, angle 5 is equal to angle 2.
Angle 5=Angle 2=115∘
5. Find angle 3: Angle 1 and angle 3 are vertically opposite angles. Therefore, angle 3 is equal to angle 1.
Angle 3=Angle 1=65∘
6. Use the property of corresponding angles again: Angle 3 corresponds to angle 8, so angle 8 is equal to angle 3.
Angle 8=Angle 3=65∘
Final Results:
- Angle 5 = 115 degrees
- Angle 8 = 65 degrees
- Angle 5 = 115 degrees
- Angle 8 = 65 degrees
Topper's Solved these Questions
Similar Questions
In Fig. 49, m∣∣n and ∠1=650. Find ∠5 and ∠8.
View SolutionIn Fig.70. if lmn and ∠1=600, find ∠2.
View SolutionIn Figure, m∣∣n and ∠1=650.Find∠5and ∠8
 View Solution
View SolutionIn Fig.72, If lm, np and ∠1=850, find ∠2.
View SolutionIn Fig.84, ABCD and AECF; ∠FCG=900 and ∠BAC=1200. Find the values of x,y and z.
View SolutionABCD is a cyclic quadrilateral in which: BCAD, ∠ADC=1100 and ∠BAC=500. Find ∠DAC ∠DBC=800 and ∠BAC=400. Find ∠BCD ∠BCD=1000and ∠ABD=700 find ∠ADB
View SolutionIn Fig 66, l∈e lm, ∠1=1200 and ∠2=1000, find out ∠3 and ∠4.
View SolutionIn Fig. 73, a transversal n cuts two lines l and m.if ∠1=700 and ∠7=800, is lm?
View SolutionIn Figure, ABCD is a parallelogram in which ∠DAO=400, ∠BAO=350 and ∠COD=650. Find: ∠ABO (ii) ∠ODC (iii) ∠ACB (iv) ∠CBD
 View Solution
View SolutionIn Fig. 68, ABCD and ∠1 and ∠2 are in the ratio 3:2. Determine all angles from 1 →8.
View Solution

