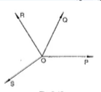
In Fig. 6.11, OP, OQ, OR and OS are four rays. Prove that ∠POQ+∠QOR+∠SOR+∠POS=360o
If we extend ray QO to T as shown in figure to point such that QT is a straight line, Then
∠POQ+∠POT=180∘→(1)--> As, angle created by a straight line is always 180∘
∠SOT+∠SOQ=180∘
As, ∠SOQ=∠SOR+∠ROQ
∠SOT+∠SOR+∠ROQ=180∘→(2)
Adding (1) and(2),
∠POQ+∠POT+∠SOT+∠SOR+∠ROQ=360∘
As,∠POT+∠SOT=∠POS,
∠POQ+∠POS+∠SOR+∠ROQ=360∘
Similar Questions
In Fig. 6.11, OP, OQ, OR and OS are four rays. Prove that ∠POQ+∠QOR+∠SOR+∠POS=360o
View SolutionIn Figure, OP, OQ, OR and OS are four rays. Prove that ∠POQ+ ∠QOR+ ∠SOR+ ∠POS=3600
View SolutionIn Fig 7.51, PR > PQand PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.

View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.

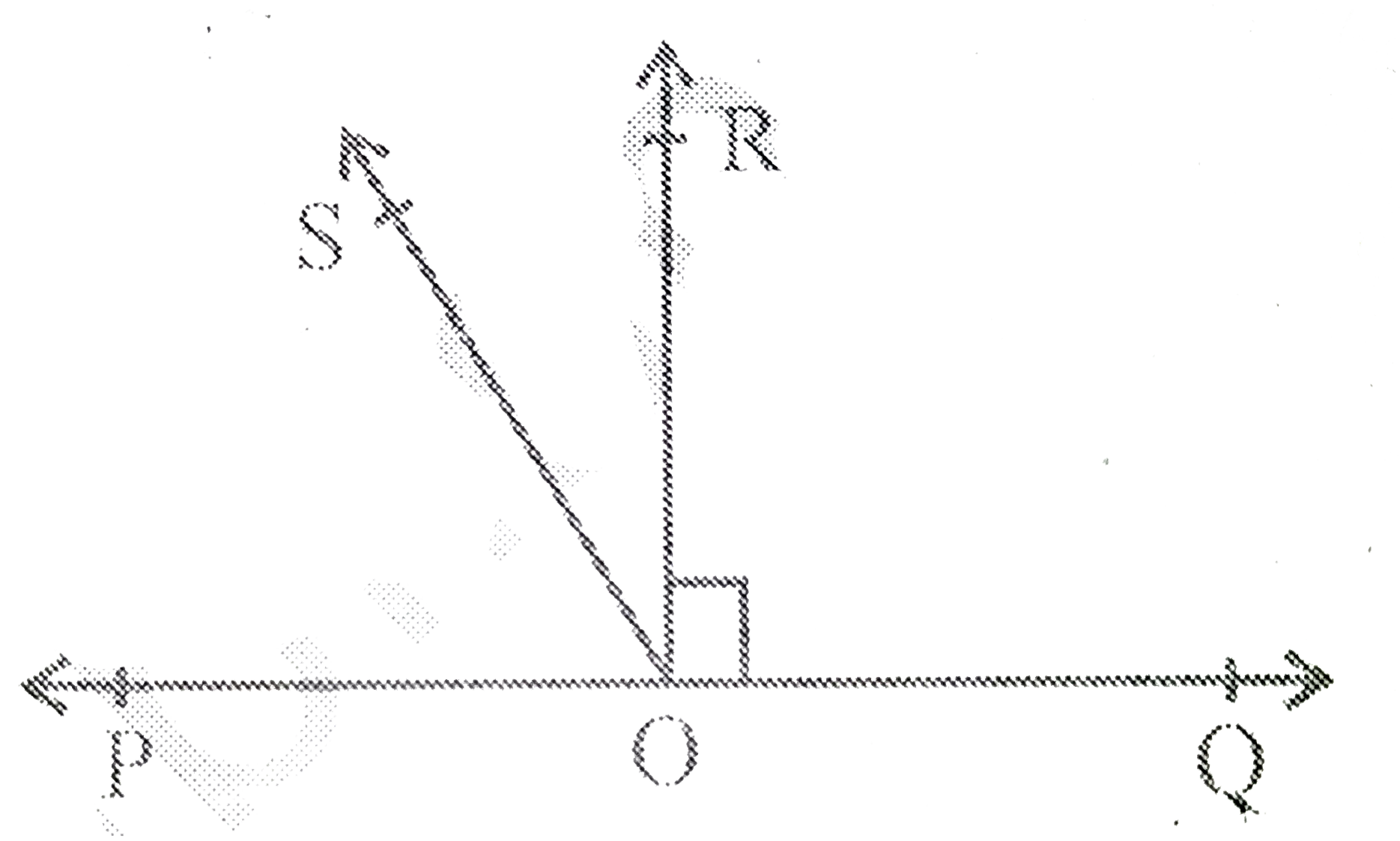
View SolutionIn Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS=12(∠QOS−∠POS).
View SolutionIn Fig. 10.95, PQ and PR are tangents drawn from P to a circle with centre O . If ∠OPQ=35o , then (FIGURE) a=30o, b=60o (b) a=35o, b=55o (c) a=40o, b=50o (d) a=45o, b=45o
View SolutionIf P + Q = R and P - Q = S, prove that R2+S2=2(P2+Q2)
View SolutionIn Fig. 4.90, if POS~ROQ , prove that PSQR . (FIGURE)
View SolutionIn Fig. 4.90, if PSQR , prove that POS~ROQ . (FIGURE)
View SolutionIn Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.

View Solution
