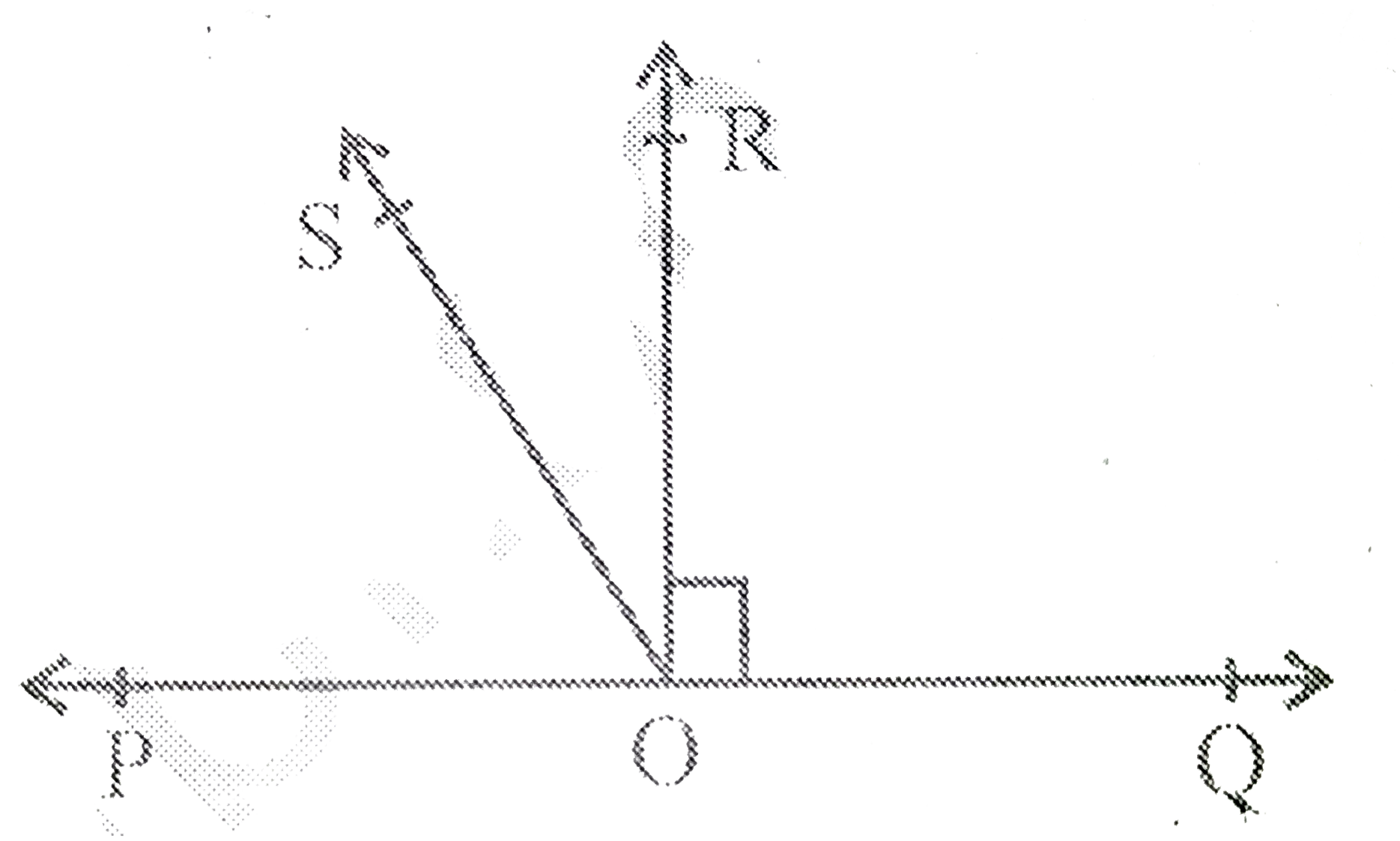
In Figure, OP, OQ, OR and OS
are four rays. Prove
that
∠POQ+ ∠QOR+ ∠SOR+ ∠POS=3600
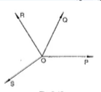
Step by step video & image solution for In Figure, O P ,\ O Q ,\ O R\ a n d\ O S are four rays. Prove that /_P O Q+\ /_Q O R+\ /_S O R+\ /_P O S=360^0 by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
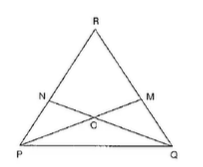
In Figure, ∠QPR= ∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN. Prove that OP=OQ, where O is the point of intersection of PM and QN
View SolutionIn Figure, PQRS is a parallelogram, PO and QO are, respectively, the angle bisectors of ∠P and ∠Q . Line LOM is drawn parallel to PQ . Prove that: PL=QM (ii) LO=OM
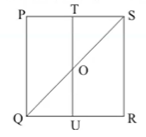
View SolutionIn Figure, PQRS is a square and T and U are, respectively, the mid-points of PS and QR . Find the area of OTS if PQ=8 cm.
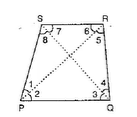
View SolutionIn Figure, PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. Prove that ∠R> ∠P and ∠S> ∠Q Given : PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. To Prove : (i) ∠R> ∠P (ii) ∠S> ∠Q Construction : Joint PR and QS
View SolutionIn figure PS is the bisector of ∠QPRof ΔPQR. Prove that QSSR=PQPR.

View SolutionIn Fig. 4.90, if POS~ROQ , prove that PSQR . (FIGURE)
View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.

View SolutionIn Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS=12(∠QOS−∠POS).
View SolutionIn Figure, ABCD is a parallelogram O s any point on AC, PQparallelAB and LMparallelAD
Prove that ar(parallelogram)DLOP)=ar(parallelogram BMOQ)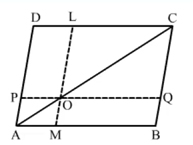
View SolutionABCD IS A PARALLELOGRAM AND O is any point in its interior. Prove that: ar (AOB)+ ar (COD)= ar (BOC)+ ar(AOD) ar (AOB)+ar (COD)=12 ar(^(gm)ABCD) Given: A parallelogram ABCD and O is a point in its interior. To Prove: ar ( AOB)+ ar(COD)=ar (BOC)+ar(AOD)
View Solution
