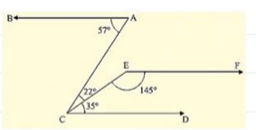
In Fig.57, show that AB∣∣EF.
To show that lines AB and EF are parallel, we can use the concept of corresponding angles. Here’s a step-by-step solution:
Step 1: Identify the Angles
In the given figure, identify the angles formed by the transversal CD intersecting the lines AB and EF. Let's denote:
- ∠ABC as angle 1
- ∠ECD as angle 2
- ∠ABE as angle 3
- ∠EFD as angle 4
Step 2: Use the Corresponding Angles Postulate
According to the Corresponding Angles Postulate, if a transversal intersects two lines such that the corresponding angles are equal, then the two lines are parallel.
Step 3: Show Angle Equality
We need to show that:
∠ABC=∠ECD
and
∠ABE=∠EFD
Step 4: Conclude Parallelism
If both pairs of corresponding angles are equal, we can conclude that:
AB∥EF
Final Statement
Thus, we have shown that lines AB and EF are parallel.
---
In the given figure, identify the angles formed by the transversal CD intersecting the lines AB and EF. Let's denote:
- ∠ABC as angle 1
- ∠ECD as angle 2
- ∠ABE as angle 3
- ∠EFD as angle 4
According to the Corresponding Angles Postulate, if a transversal intersects two lines such that the corresponding angles are equal, then the two lines are parallel.
We need to show that:
∠ABC=∠ECD
and
∠ABE=∠EFD
If both pairs of corresponding angles are equal, we can conclude that:
AB∥EF
Thus, we have shown that lines AB and EF are parallel.
Topper's Solved these Questions
Similar Questions
In Fig.57, show that AB∣∣EF.
View SolutionIn Fig. 75, Show that ABEF.
View SolutionIn Fig, Show that ABEF.
 View Solution
View SolutionIn quadrilateral ACBD, AC = ADand AB bisects ∠A(see Fig. 7.16). Show that ΔABC≅ΔABD
 View Solution
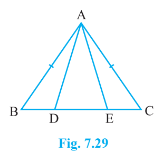
View SolutionIn an isosceles triangle ABC with AB=AC, D and E are points on BCsuch that BE=CD(see Fig. 7.29). Show that AD=AE
 View Solution
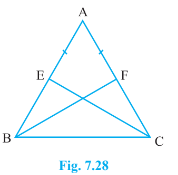
View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC(see Fig. 7.28). Show that BF = C E.
 View Solution
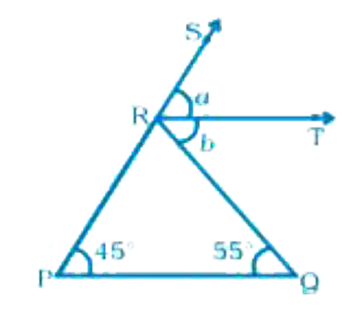
View SolutionIn Fig. 5.57, PQ || RT. Find the value of a + b.
 View Solution
View SolutionIn Figure, state the three pairs of equal parts in ΔABCandΔEOD. IsΔABC≅ΔEOD? Why?
 View Solution
View SolutionIn figure, if ΔABE≅ΔACD, show that ΔADE~ΔABC.
 View Solution
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
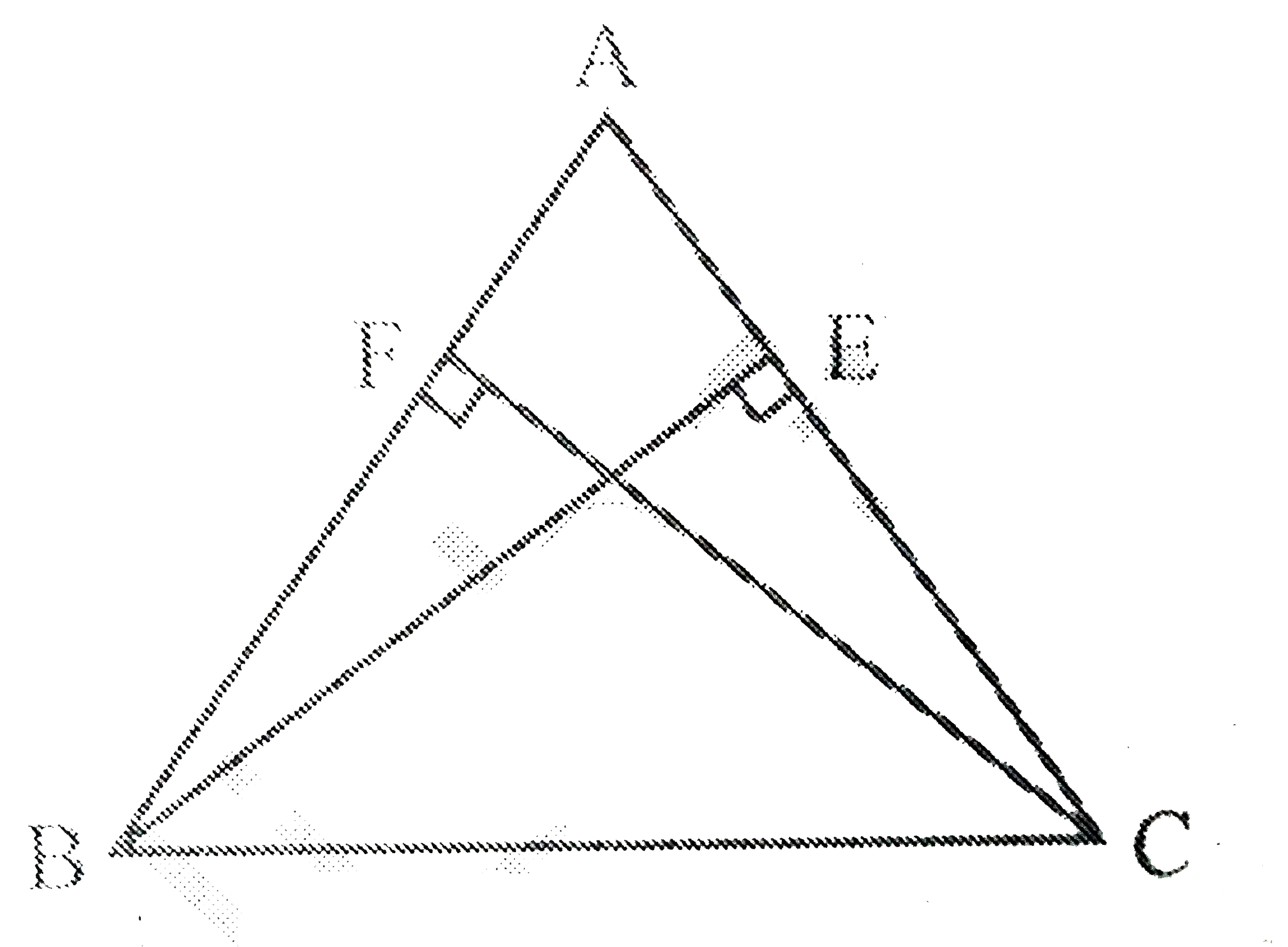 View Solution
View Solution

