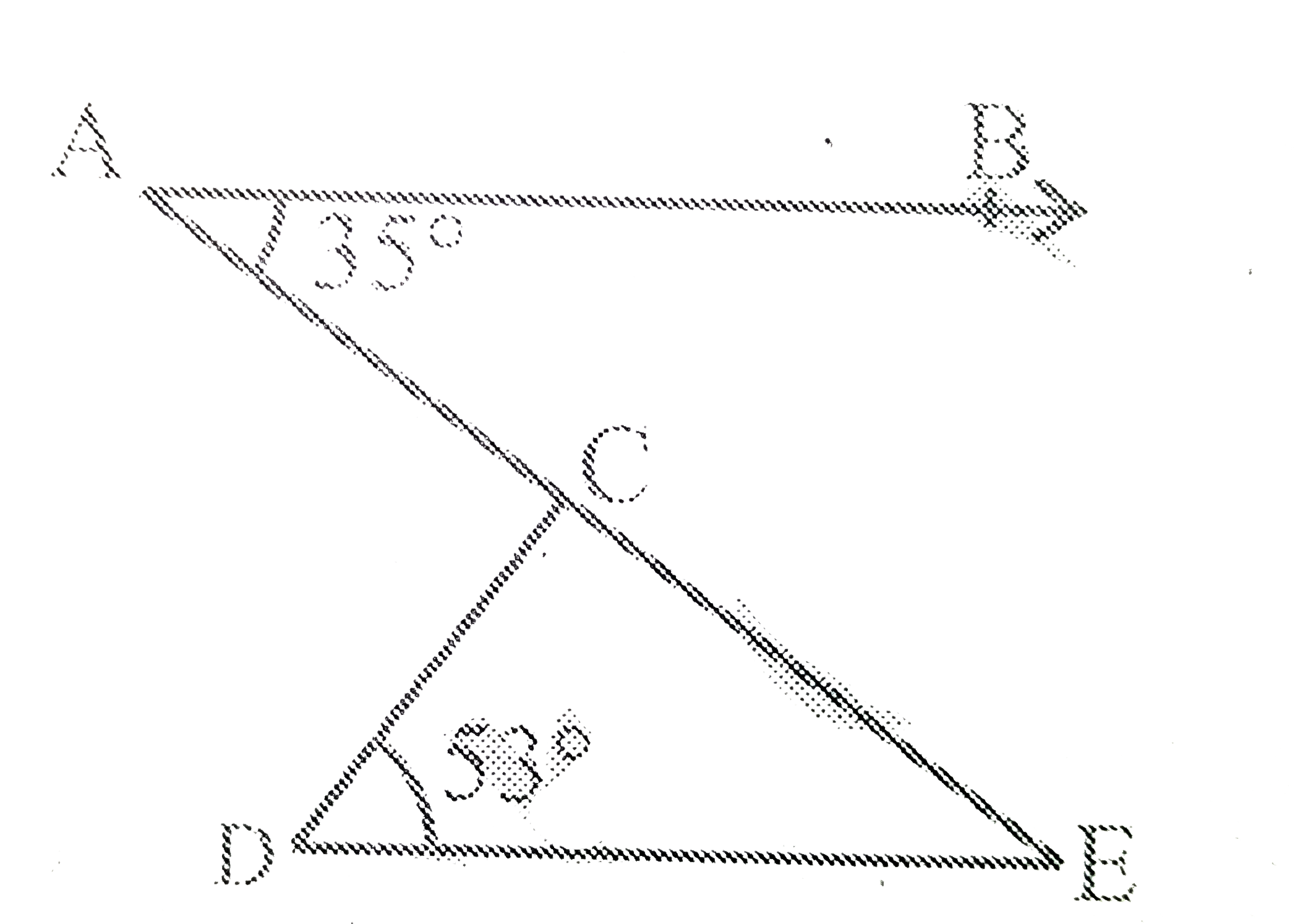
In Fig.74, if ABCD, ∠CAB=490, ∠CBD=270 and ∠BCD=1120, then the values of x and y are x=41, y=90, (b) x=41, y=63, x=63, y=41, (d) x=90, y=41,
To solve the problem step by step, we will use the properties of parallel lines and triangles.
Step 1: Identify the angles
We are given:
- ∠CAB=49∘
- ∠CBD=27∘
- ∠BDC=112∘
We need to find the values of x (which is ∠ABC) and y (which is ∠ACB).
Step 2: Use the property of parallel lines
Since AB is parallel to CD and BD is a transversal, we can use the property that states the sum of the interior angles on the same side of the transversal is 180∘.
Thus, we have:
∠ABD+∠BDC=180∘
Step 3: Express ∠ABD
We know that:
∠ABD=x+27∘
So we can write the equation:
(x+27∘)+112∘=180∘
Step 4: Solve for x
Now, simplify the equation:
x+139∘=180∘
Subtract 139∘ from both sides:
x=180∘−139∘
x=41∘
Step 5: Use the angle sum property of triangle ABC
Now, we will apply the angle sum property of triangle ABC, which states that the sum of the angles in a triangle is 180∘:
x+∠CAB+y=180∘
Substituting the known values:
41∘+49∘+y=180∘
Step 6: Solve for y
Combine the known angles:
90∘+y=180∘
Subtract 90∘ from both sides:
y=180∘−90∘
y=90∘
Final Values
Thus, we have:
- x=41∘
- y=90∘
Conclusion
The values of x and y are:
- x=41∘
- y=90∘
We are given:
- ∠CAB=49∘
- ∠CBD=27∘
- ∠BDC=112∘
Since AB is parallel to CD and BD is a transversal, we can use the property that states the sum of the interior angles on the same side of the transversal is 180∘.
∠ABD+∠BDC=180∘
We know that:
∠ABD=x+27∘
So we can write the equation:
(x+27∘)+112∘=180∘
Now, simplify the equation:
x+139∘=180∘
Subtract 139∘ from both sides:
x=180∘−139∘
x=41∘
Now, we will apply the angle sum property of triangle ABC, which states that the sum of the angles in a triangle is 180∘:
x+∠CAB+y=180∘
Substituting the known values:
41∘+49∘+y=180∘
Combine the known angles:
90∘+y=180∘
Subtract 90∘ from both sides:
y=180∘−90∘
y=90∘
Thus, we have:
- x=41∘
- y=90∘
The values of x and y are:
- x=41∘
- y=90∘
Topper's Solved these Questions
Similar Questions
In Fig.70, if ABCD, then the value of x and y are x=24, y=48 (b) x=34, y=68 x=24, y=68 (d) x=34, y=48
View SolutionIn Figure, ∠BAD=780, ∠DCF=x0and ∠DEF=y0. Find the value of x and y
View SolutionIn Fig.69, if ABCD, then the value of x and y are x=106, y=307 (b) x=307, y=106 x=107, y=306 (d) x=105, y=308
View SolutionIn the given figure, the value of x and y are
(a) x=20, y=130
(b) x=40, y=140
(c) x=20, y=140
(d) x=15, y=140
View SolutionIn Fig.84, AB||CD and AE||CF; ∠FCG=900 and ∠BAC=1200. Find the values of x,y and z.
View SolutionIn Fig.71, if ABCD, then the values of x, y and z are x=56, y=47, z=77 (b) x=47, y=56, z=77 x=77, y=56, z=47 (d) x=56, y=77, z=47
View SolutionIn the given figure, if AB∣∣CD, the values of x and y are
(a) x=21, y=28
(b) x=21, y=38
(c) x=38, y=21
(d) x=22, y=38
View SolutionIn a parallelogram ABCD, if ∠A=(3x−20)0, ∠B (y+15)0, ∠C=(x+40)0, then find the values of x and y
View SolutionIn Fig. 6.41, if AB∣∣DE,∠BAC=35∘ and ∠CDE=53∘, find ∠DCE.
View SolutionIn Figure, If AB||CD, CD||EF and y:z=3:7, find x.
View Solution
