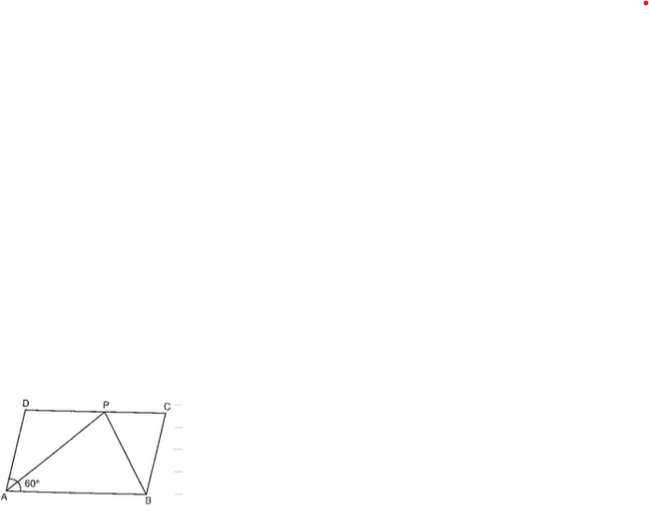
In Figure, ABCD is a parallelogram in which ∠A=60∘ . If the bisectors of ∠A and ∠B meet at P, prove that AD=DP,PC=BC and DC=2AD. Figure
"given,AP bisects∠A
Then,
∠DAP=∠PAB=30∘------ ( 1 )
We know that in parallelogram adjacent angles are supplementary
so, ∠A+∠B=180∘
60∘+∠B=180∘
∠B=120∘
BP bisects angle B
Then,
∠PAB=∠PBC=60∘---- ( 2 )
∠PAB=∠APD=30∘[ Alternate angles ]---- ( 3 )
∠DAP=∠APD=30∘[ From ( 1 ) and ( 3 ) ]
so,
AD=DP[Since base angles are equal ]
Similarly, ∠PBA=∠BPC=60∘[ Alternate angles ]--- ( 4 )
∠PBC=∠BPC=60∘[ From ( 2 ) and ( 4 ) ]
so, PC=BC [ Since base angles are equal
DC=DP+PC
DC=AD+BC[ Since,DP=AD,PC=BC]
DC=AD+AD[ Opposite sides of parallelogram are equal ]
so,
DC=2AD"
Topper's Solved these Questions
Similar Questions
In Figure, ABCD is a parallelogram in which ∠A=600 . If the bisectors of ∠A and ∠B meet at P, prove that AD=DP,PC=BC and DC=2AD.
 View Solution
View SolutionABCD is a parallelogram in which ∠A=70∘ Compute ∠B, ∠C and ∠D
View SolutionABCD is a parallelogram in which ∠A=70∘. Compute ∠B, ∠C and ∠D.
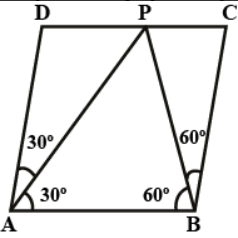
View SolutionIn Figure, ABCD is a parallelogram and ∠DAB=600. If the bisectors AP and BP of angles A and B respectively, meet at P on CD, prove that P is the mid-point of CD
 View Solution
View SolutionIn a parallelogram ABCD, the bisector of ∠A also bisects BC at X Prove that AD=2AB
View SolutionIn a parallelogram ABCD, if ∠D=115∘, then write the measure of ∠A
View SolutionIf ABCD is a rhombus with ∠ABC=56∘, find the measure of ∠ACD
View SolutionIn a parallelogram ABCD, the bisector of ∠A also bisects BC at X Find AB:AD
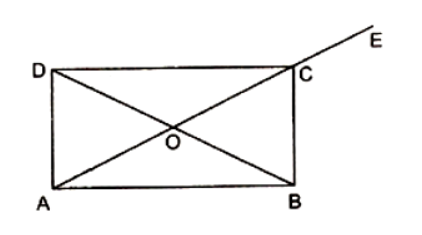
View SolutionIn Figure, ABCD is a rectangle in which diagonal AC is produced to E. If ∠ECD=1460, find ∠AOB
 View Solution
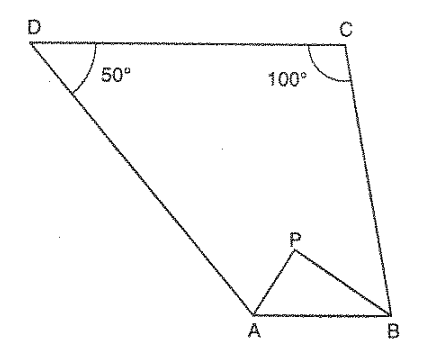
View SolutionIn Figure, the bisectors of ∠A and ∠B meet at a point P. If ∠C=1000 and ∠D=500, find the measure of ∠APB
 View Solution
View Solution

