In Figure, ABC
is an isosceles triangle in which AB=AC.CPAB
and AP
is the bisector of exterior ∠CAD
of ABC
. Prove that
∠PAC=∠BCA
and (ii)
ABCP
is a parallelogram.
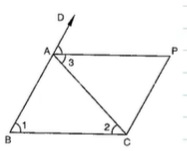
Step by step video & image solution for In Figure, A B C is an isosceles triangle in which A B=A CdotC P A B and A P is the bisector of exterior /_C A D of A B C . Prove that /_P A C=/_B C A and (ii) A B C P is a parallelogram. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In figure AB=AC and CP∣∣BA and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA (ii) ABCP is a parallelogram
View SolutionABC is an isosceles triangle in which AB=AC. AD bisects exterior angle PAC and CD∣∣AB. Show that(i) ∠DAC=∠BCA and (ii) ABCD is a parallelogram.
View SolutionIf ABC is an isosceles triangle such that AB=AC and AD is an altitude from A on BC . Prove that (i) ∠B=∠C (ii) AD bisects BC (iii) AD bisects ∠A
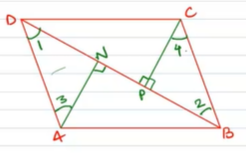
View SolutionIn Figure, AN and CP are perpendicular to the diagonal BD of a parallelogram ABCD. Prove that : ADN≅CBP (ii) AN=CP
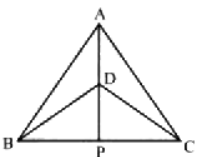
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD ≅ACD (ii) ABP ≅ACP
View SolutionABCD is a cyclic quadrilateral whose diagonals AC and BD intersect at P. If AB=DC, prove that:
(i)PAB ≅PDC
(ii)PA=PD and PC=PB (iii) AD∣∣BC
View SolutionABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD≅ACD (ii) ABP≅ACP AP bisects ∠A as well as ∠D AP is perpendicular bisector of BC.
View SolutionABCD is a cyclic quadrilateral whose diagonals ACandBD intersect at P . If AB=DC, Prove that : PAB≅PDC PA=PDandPC=PB ADBC
View SolutionIf P is any point in the interior of a parallelogram ABCD, then prove that area of the triangle APB is less than half the area of parallelogram.
View SolutionIn ABC , ∠A is obtuse, PB⊥AC and QC⊥AB . Prove that: AB×AQ=AC×AP (ii) BC2=(AC×CP+AB×BQ)
View Solution
