In Figure, ABCD isa trapezium in which side AB is a parallel to side DC and E is the mid-point of side AD. If F is a point on the side BC such that the segment EF is parallel to side DC . Prove that F is the mid point of BC and EF=12(AB+DC).
Given ABCD is a trapezium in which AB||CD. Also, E and F are respectively the mid-points of sides AD and BC.
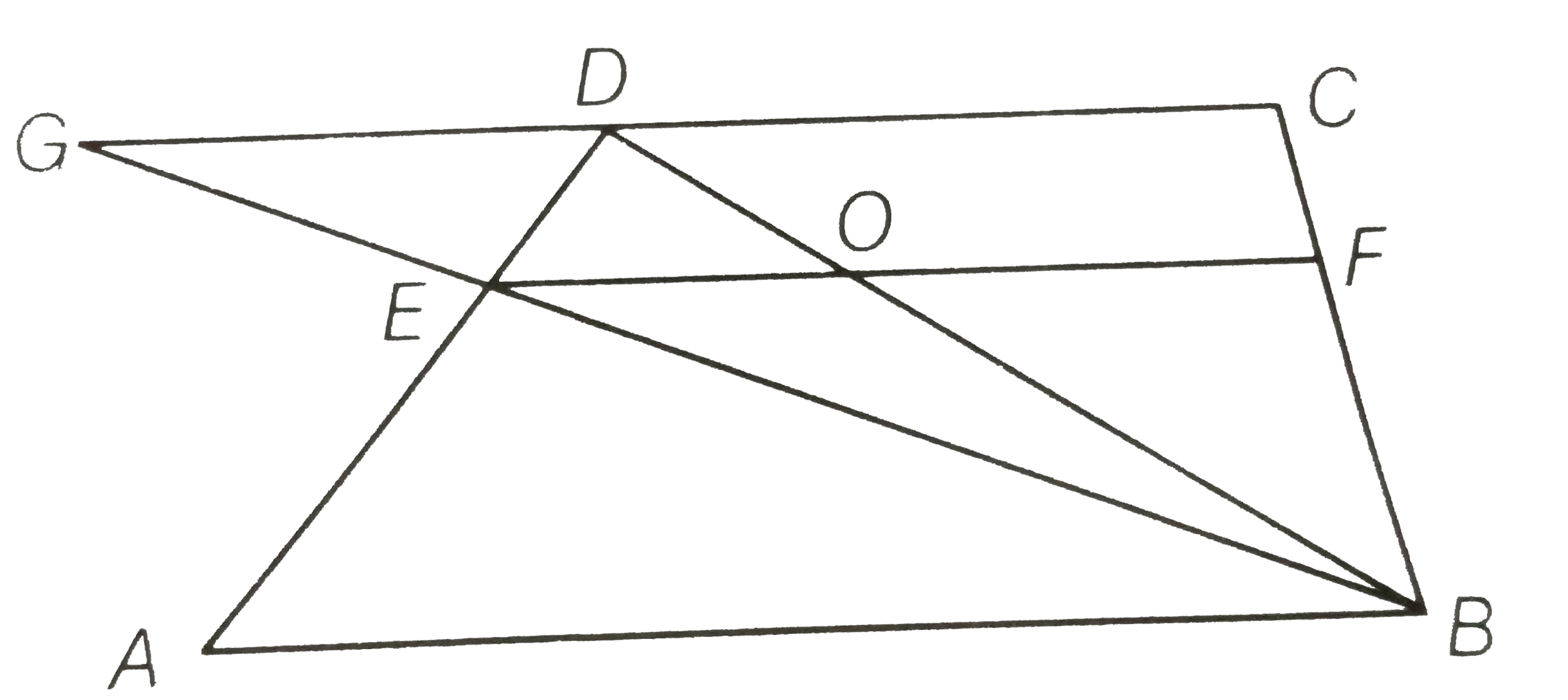
Construction Join BE and produce it to meet CD produced at G, also draw BD which intersects EF at O.
To prove EF||AB and EF =12(AB+CD).
Proof In ΔGCB, E and F are respectively the mid-points of BG and BC, then by mid-point theorem,
EF∣∣GC
But GC||ABorCD||AB [given]
∴ EF∣∣AB
In ΔADB, AB||EO and E is the mid-point of AD.
Therefore by converse of mid-point theorem, O is mid-point of BD.
Also, EO=12AB ...(i)
In ΔBDC, OF||CD and O is the mid-point of BD.
∴ OF=12CD [ by converse of mid-point theorem]...(ii)
On addillng Eqs. (i) and (ii), we get
EO+OF=12AB+12CD
⇒ EF=12(AB+CD) Hence proved.
Topper's Solved these Questions
Similar Questions
In Figure, ABCD isa trapezium in which side AB is a parallel to side DC and E is the mid-point of side AD. If F is a point on the side BC such that the segment EF is parallel to side DC . Prove that F is the mid point of BC and EF=12(AB+DC).
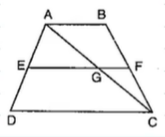
View SolutionIn the figure ABCD is a trapezium in which side AB is parallel to side DC and E is the midpoint of side AD. If F is a point on the side BC such that the line segment EF is parallel to DC.Prove that Fis the mid-point of BC and EF=12(AB+DC)
View SolutionIn Figure, ABCD is a rectangle with sides AB=10cmandAD=5cm Find the area of EFG
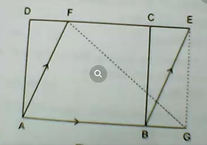
View SolutionAB and CD are the parallel sides of a trapeziuml. E is the mid-point of AD. A line through E and parallel to side AB meets the line BC at point F. Prove that F is the mid-point of BC.
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(BOE)=18ar(ABC)
View SolutionIn figure D is a point on side BC of a ΔABCsuch that BDCD=ABAC. Prove that AD is the bisector of ∠BAC.

View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE trisect (divide into three equal parts) the diagonal BD .
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE, prove that ar ( BOE)=18ar ( ABC)
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid=points of sides AB and DC respectively. Show that AXCY is a parallelogram.
View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of △BED=14areaof△ABC. GIVEN : A ABC,D is the mid-point of BC and E is the mid-point of the median AD. TO PROVE : ar(△BED)=14ar(△ABC).
View Solution
