Points P and Q have been taken on opposite sides AB and CD, respectively of a parallelogram ABCD such that AP=CQ. Show that AC and PQ bisect each other.
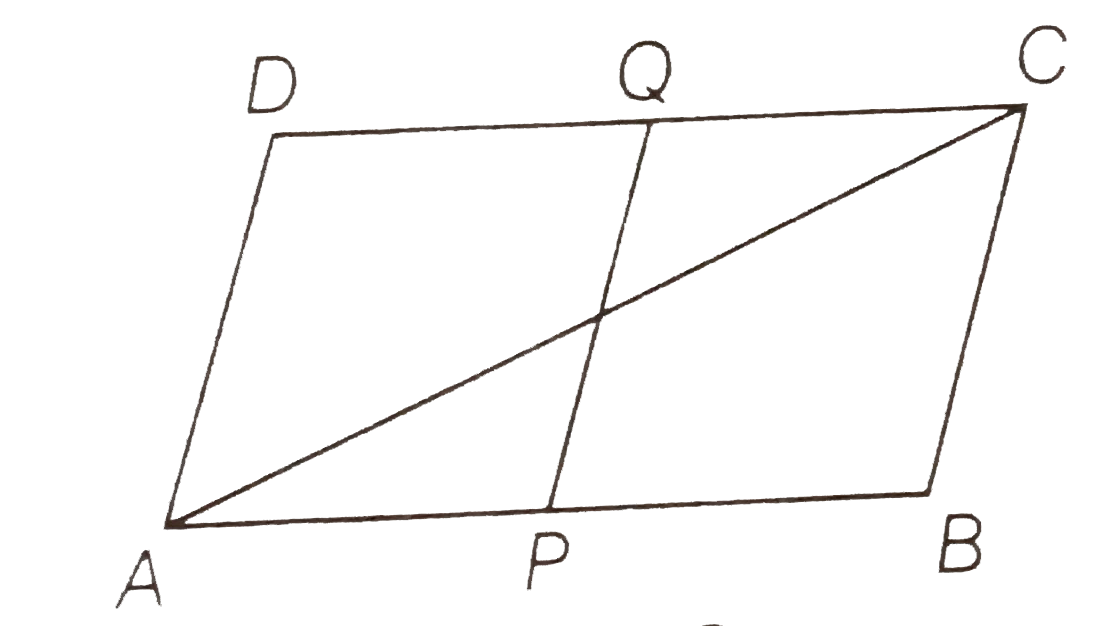
Given ABCD is a parallelogram and AP = CQ
To show AC and PQ bisect each each other.

Proof In ΔAMP and ΔCMQ,
∠MAP=∠MCQ [alternate interior angles]
AP=CQ [given]
and ∠APM=∠CQM [alternate interior angles]
∴ ΔAMP≅ΔCMQ [by ASA congruence rule]
⇒ AM=CM [by CPCT rule]
and PM=MQ [by CPCT rule]
Hence, AC and PQ bisect each other. Hence proved.
Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram. Points P and Q are taken on the sides AB and AD respectively and the parallelogram PRQA is formed. If ∠C=45∘, find ∠R.
View SolutionP and Q are points on opposite sides AD and BC of a parallelogram ABCD such that PQ passes through the point of intersection O of its diagonals AC and BD. Show that PQ is bisected at O.
View Solution
Knowledge Check
- Question 1 - Select One
If P and Q are the middle points of the sides BC and CD of the parallelogram ABCD, then AP+AQ is equal to
AACB12ACC23ACD32AC
P and Q are points on the sides AB and AC respectively of a △ABC. If AP= 2cm, PB = 4cm AQ= 3cm and QC= 6cm. Show that BC= 3PQ.
View SolutionP and Q are the points on sides AB and AC respectively of a ΔABC , such that PQ||BC .If AP∣PB=2:3 and AQ=4 cm , then the length of AC is ….. Cm .
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at EandF . Prove that EBFD is a parallelogram.
View SolutionP and Q are the mid-point of the oposite sides AB and CD of a parallelogram ABCD. AQ interects DP at S and BQ interects CP at R. Show that PQRS is a parallelogram.
 View Solution
View SolutionM and N are points on opposite sides AD and BC of a parallelogram ABCD such that MN passes through the point of intersection O of its diagoinals AC and BD. Show that MN is bisected at O.
View SolutionABCD is a parallelogram. Tow points P and Q are taken on sides AD and BC respectively such that AP 13ADandCQ=13BC. Prove that □AQCP is a parallelogram.
View SolutionABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:
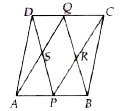
(i) APCQ is a parallelogram.View Solution

