P, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC=BD and AC⊥BD. Prove that PQRS is a square.
Given In quadrilateral ABCD, P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively.
Also, AC=BDandAC⊥BD.
To prove PQRSk is a square.
Proof Now, in ΔADC, S and R are the mid points of the sides AD and DC respectively, then by mid-point theorem,
SR∣∣ACandSR=12AC ...(i)
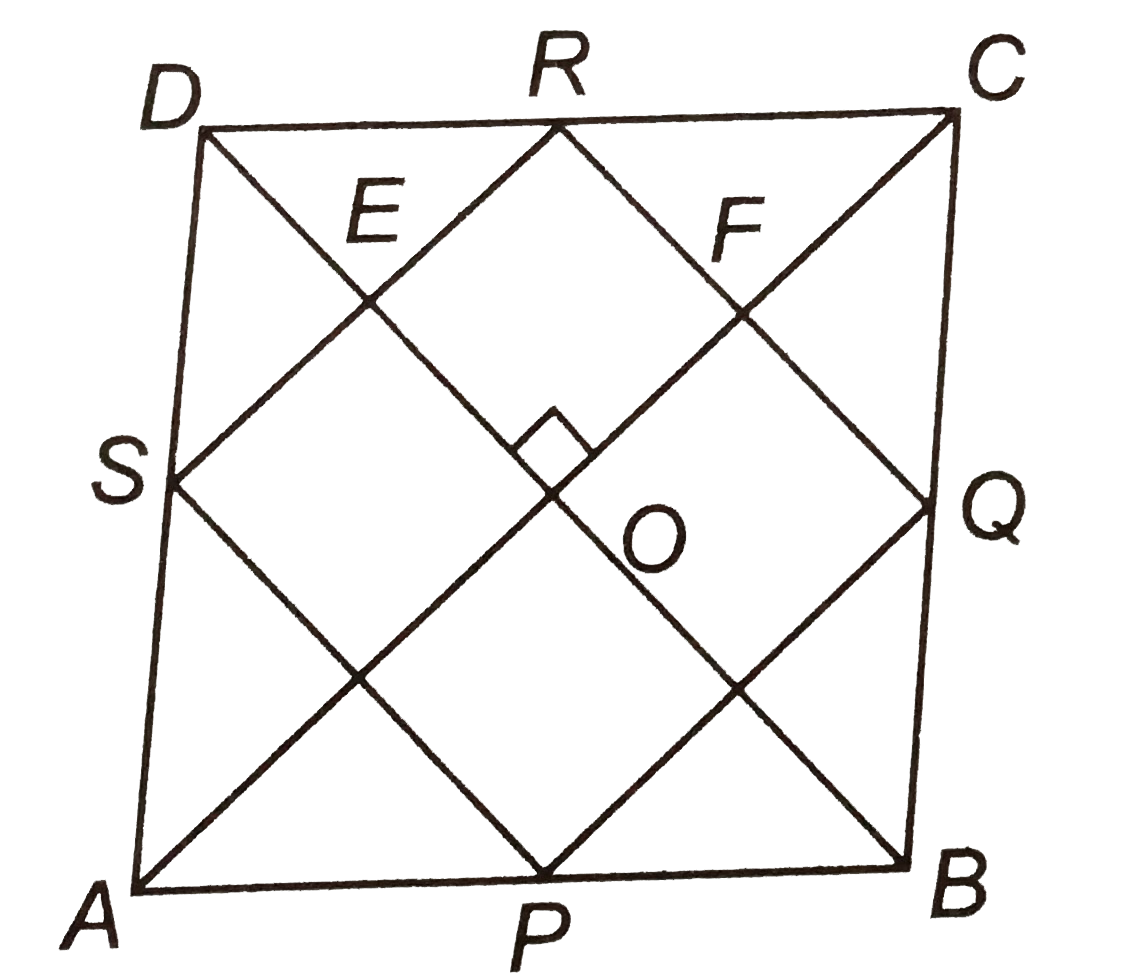
In ΔABC, P and Q are the mid-points of AB and BC, then by mid-point theorem,
PQ∣∣ACandPQ=12AC ...(ii)
From Eqs. (i) and (ii), PQ∣∣SRandPQ=SR=12AC ...(iii)
Similarly, in ΔABD, by mid-point theorem,
SP∣∣BDandSP=12BD=12AC [given, AC=BD]...(iv)
and ΔBCD, by mid-point theorem,
RQ∣∣BDandRQ=12BD=12AC [given, BD=AC]...(v)
From Eqs. (iv) and (v),
SP=RQ=12AC ...(vi)
From Eqs. (iii) and (vi), ltBrgt PQ=SR=SP=RQ
Thus, all four sides are equal.
Now, in quadrilateral OERF, OE||FRandOF||ER
∴ ∠EOF=∠ERF=90∘
[∵AC⊥DB⇒=∠DOC=∠EOF=90∘ as opposite angles of a parallelogram]
∴ ∠QRS=90∘
Similarly, ∠RQS=90∘
So, PQRS is a square. Hence proved.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
M and N are the mid-points of the diagonals AC and BD respectively of quadrilateral ABCD, then AB+AD+CB+CD is equal to
A2 MNB2NMC4 MND4 NM
If ABCD is a quadrilateral in which ABCD and AD=BC, prove that ∠A =∠B.
View SolutionLet P, Q, R, S be respectively the midpoints of the sides AB, BC, CD and DA of quad. ABCD Show that PQRS is a parallelogram such that
ar(||gm PQRS)=12ar(quad. ABCD).
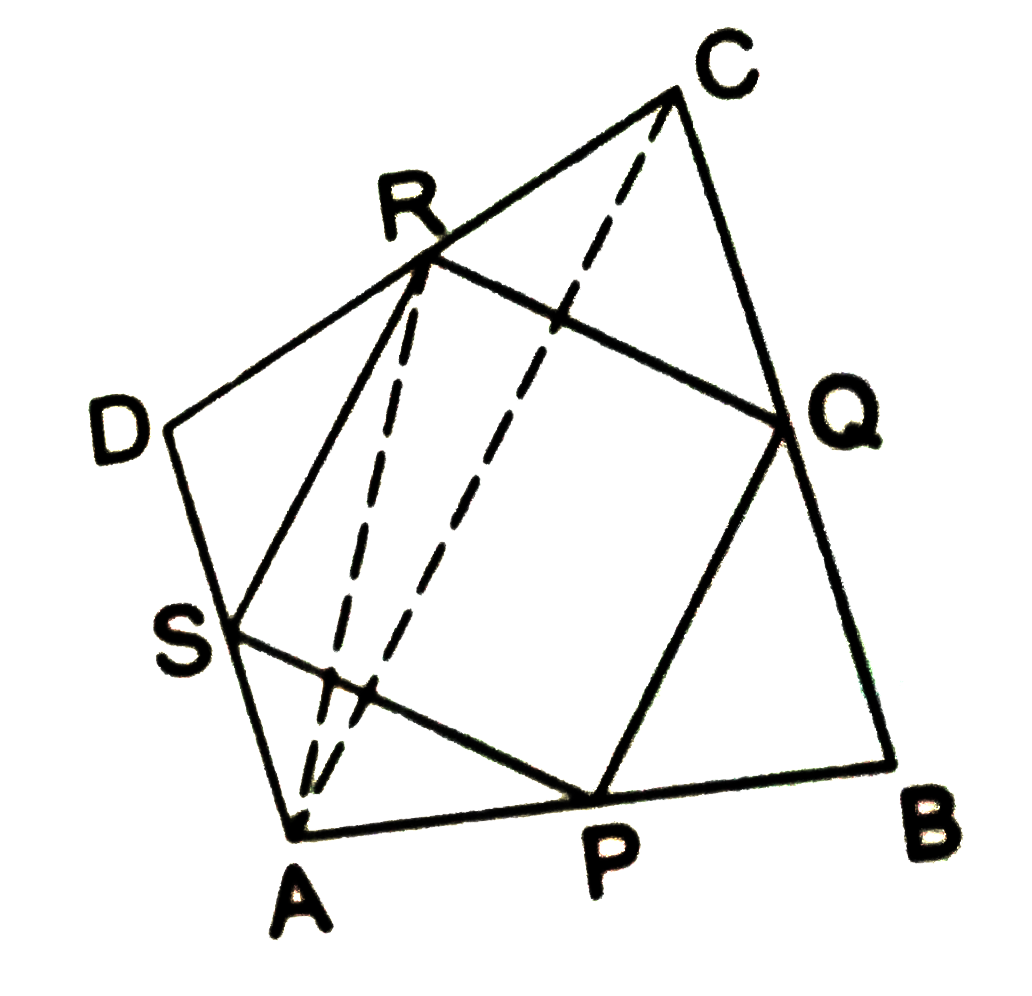 View Solution
View SolutionP, Q, R, S are respectively the midpoints of the sides AB, BC, CD and DA of ||gm ABCD. Show that PQRS is a parallelogram and also show that
ar(|| gm PQRS)=12×ar(∣∣gmABCD).
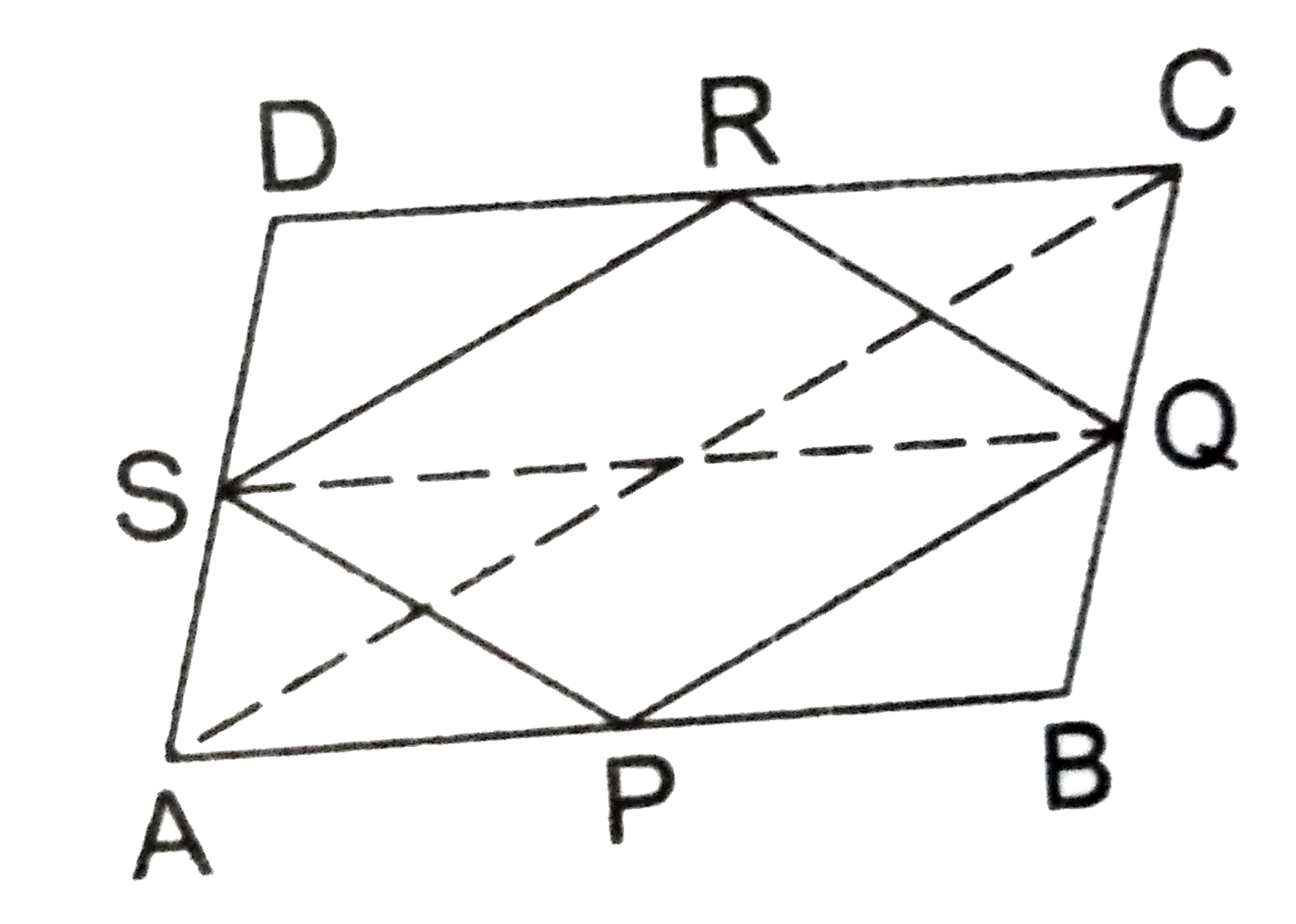 View Solution
View SolutionK, L, M and N are points on the sides AB, BC, CD and DA respectively of a square ABCD such that AK = BL = CM = DN. Prove that KLMN is a square.
View SolutionThe midpoints of the sides AB,BC,CDandDA of a quadrilateral ABCD are joined to form a quadrilateral. If AC=BDandAC⊥BD then prove that the quadrilateral formed is a square.
View SolutionABCD is a quadrilateral; P,Q,RandS are the points of trisection of side AB,BC,CDandDA respectively and are adjacent to AandC ; prove that PQRS is parallelogram.
View SolutionP and Q are the mid-point of the oposite sides AB and CD of a parallelogram ABCD. AQ interects DP at S and BQ interects CP at R. Show that PQRS is a parallelogram.
 View Solution
View Solution
