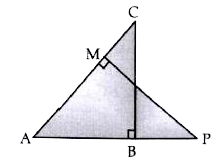
In figure ABC and AMP are two right triangles, right angles at B and M respectively. Prove that(i) $Δ A B C ~ Δ A M P$ (ii) $\frac{C A}{P A} = \frac{B C}{M P}$

Video Solution

Text Solution

Verified by Experts

(i)In $Δ A B C$ and $Δ A M P$
$∠ B A C = ∠ P A M$ , As both angles are common.
$∠ A B C = ∠ A M P = 90^{\circ}$
As these two angles are equal, third angle will also be equal for these two triangles.
As, all three angles are equal, we can say that
$Δ A B C ~ Δ A M P$
(ii)It also means,
$\frac{A B}{A M} = \frac{C A}{P A} = \frac{B C}{M P}$
Hence, $\frac{C A}{P A} = \frac{B C}{M P}$

|

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Similar Questions

Knowledge Check

Question 1 - Select One
If triangle ABC is right angled at C, then the value of sec (A+B) is
A $0$
B $1$
C $\frac{2}{\sqrt{3}}$
DNot defined
Question 2 - Select One
ABC is a right angled triangle. B being the right angle. Mid-points of BC and AC are respectively B' and A'. Area of $Δ A' B' C'$ is
A $\frac{1}{2} \times area of Δ A B C$
B $\frac{2}{3} \times area of Δ A B C$
C $\frac{1}{4} \times area of Δ A B C$
D $\frac{1}{8} \times area of Δ A B C$
Question 3 - Select One
If in a triangle ABC, right angled at B, s-a=3, s-c=2, then the values of a and c are respectively
A2,3
B3,4
C4,3
D6,8

Recommended Questions

Home
Ask Doubt
Profile