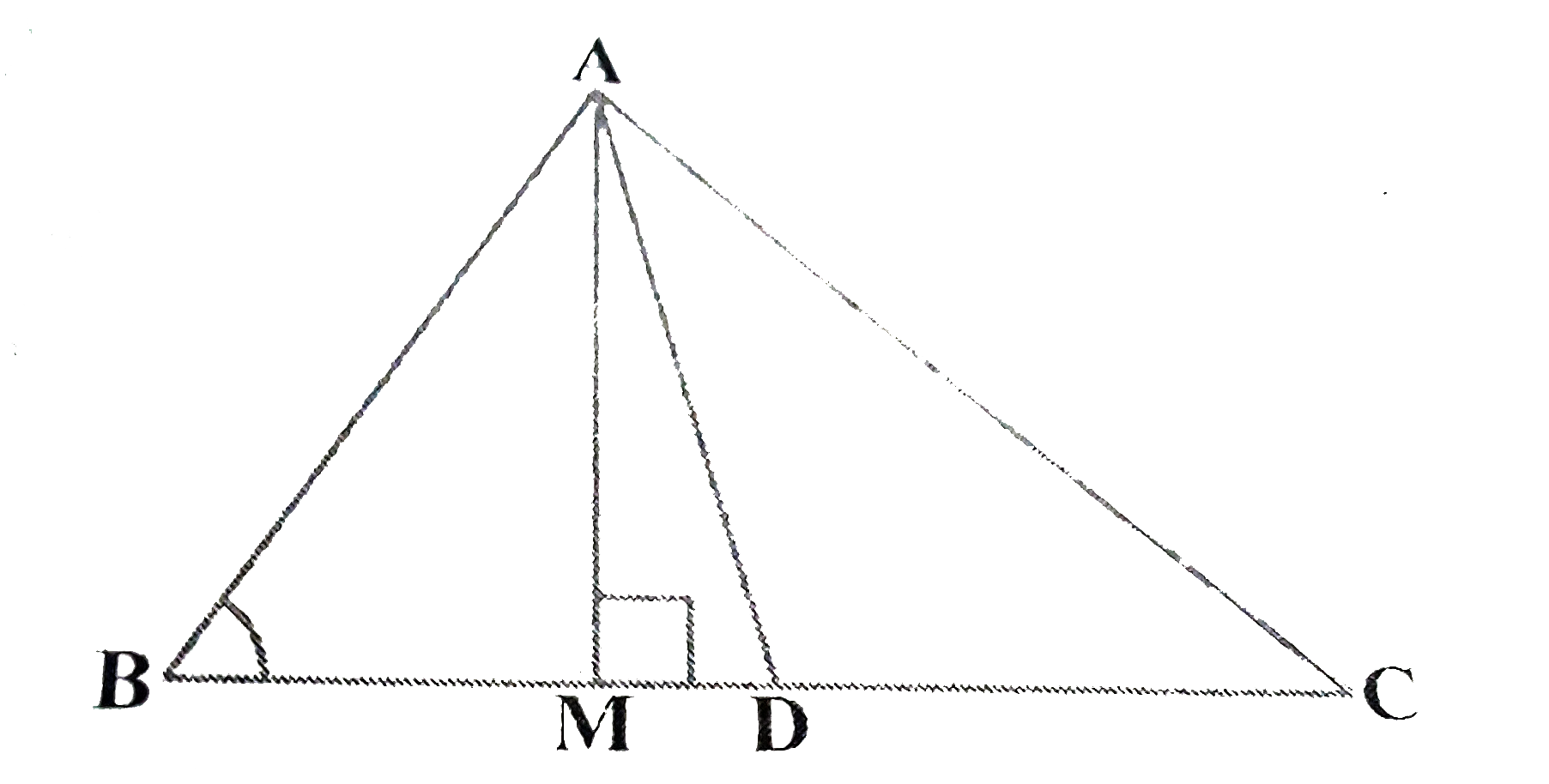
In figure, ABC is a triangle in which and . Prove that .

Using Pythagoras Theorem In as
[∵ In ΔADB, ]
Hence it is proved that
Topper's Solved these Questions
Similar Questions
In figure, ABC is triangle in which ∠ABC>90∘ and AD⊥CBproduced. Prove that AC2=AB2+BC2+2BC.BD.

View SolutionABC is a triangle in which AB=AC and D is any point in BC . Prove that AB2−AD2=BDCD .
View SolutionIn Figure, ∠B of ABC is an acute angle and AD⊥BC , prove that AC2=AB2+BC2−2 BC×BD
View SolutionIf ABCD is a quadrilateral in which ABCD and AD=BC, prove that ∠A =∠B .
View SolutionIn Figure, ABC is an obtuse triangle, obtuse angled at B . If AD⊥CB , prove that AC2=AB2+BC2+2 BC×BD .
View SolutionIn ABC, ∠A=60o . Prove that B C^2=A B^2+A C^2-A B.A C .
View SolutionIn figure ∠ACB=90∘and CD⊥AB. Prove that BC2AC2=BDAD.
View SolutionIn fig., if AD⊥BC, prove thatAB2+CD2=BD2+AC2.
View SolutionIn figure, AD is a median of a triangle ABC and AM⊥BC. Prove that:
(i) AC2=AD2+BC.DM+(BC2)2
(ii) AB2=AD2−BC.DM+(BC2)2
(iii) AC2+AB2=2AD2+12BC2
View SolutionIn Figure, AD⊥BC and BD=13CD. Prove that 2CA2=2AB2+BC2
View Solution
