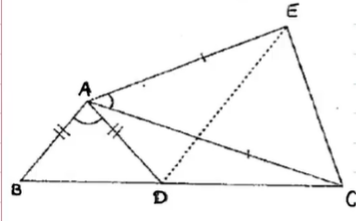
In figure, AB||DE, AB=DE, AC||DF and AC=DF. Prove that BC||EF and BC=EF.
Video Solution
Text Solution
Given In figure AB||DE and AC||DF, also AB=DE and AC=DF
To prove BC∣∣EFandBC=EF
Proof In quadrilateral ABED,
AB∣∣DEandAB=DE
So, ABED is a parallelogram.
∴ AD∣∣BEandAD=BE ...(i)
Now, in quadrilateral ACFD,
AC∣∣FDandAC=FD
Thus, ACFD is a parallelogram.
∴ AD∣∣CFandAD=CF ...(ii)
From Eqs. (i) and (ii),
AD=BE=CFandCF∣∣BE ...(iii)
Now, in quadrilateral BCFE,
BE=CF
and BE∣∣CF [from Eq. (iii)]
So, BCFE is a parallelogram.
∴ BC=EFandBC∣∣EF Hence proved.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given figure.AB||DE, AB=DE, AC||DF and AC=DF.Then which of the following is correct.
 ABC||EFBBC=EFCBothAandBDNone
ABC||EFBBC=EFCBothAandBDNone
It is given figure, AB||DE||andBD∣∣EF.
Prove that DC2=CF×AC.
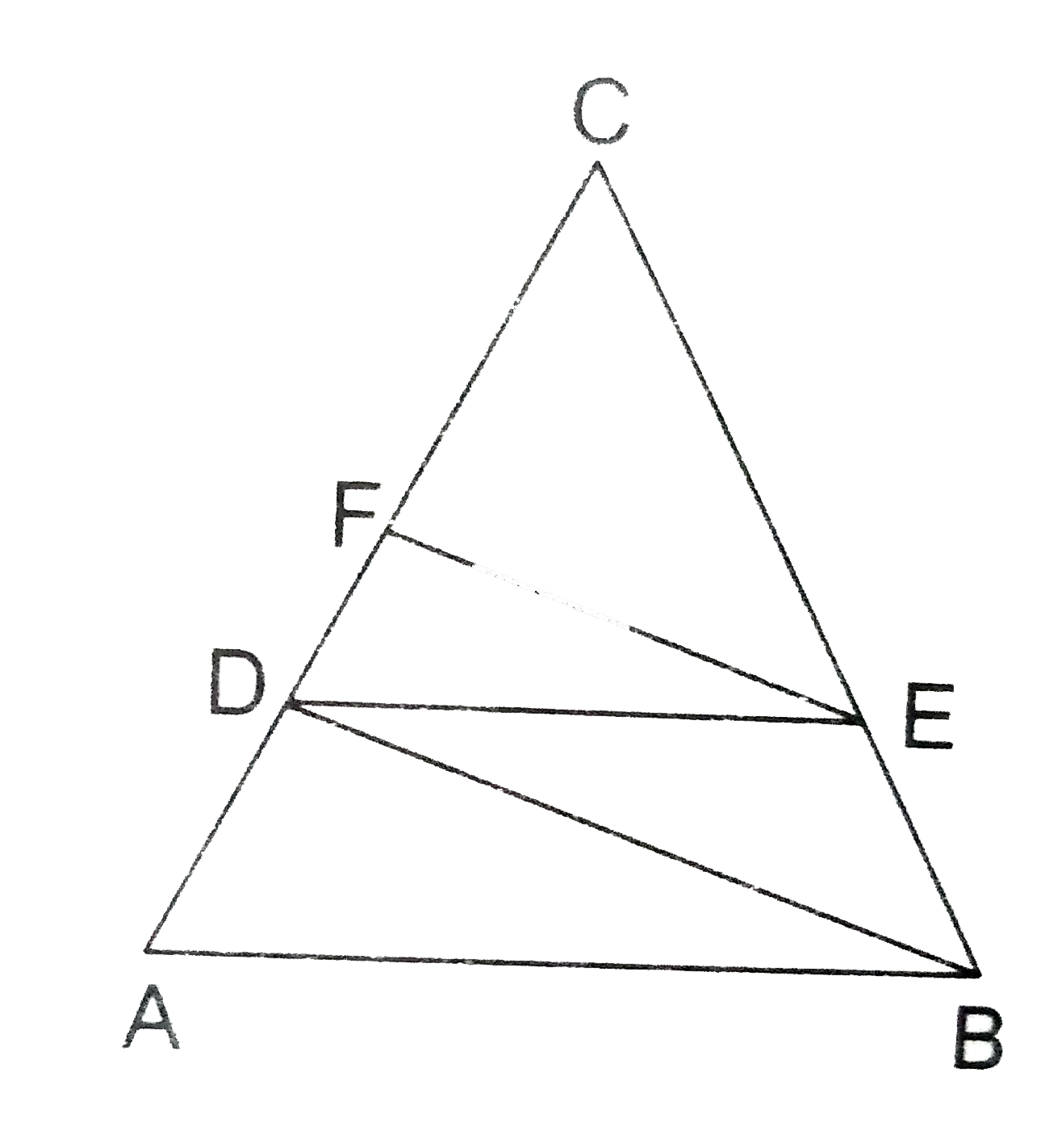
View SolutionIn the given figure, AC=AE,AB=AD and ∠BAD=∠EAC. Prove that BC=DE.
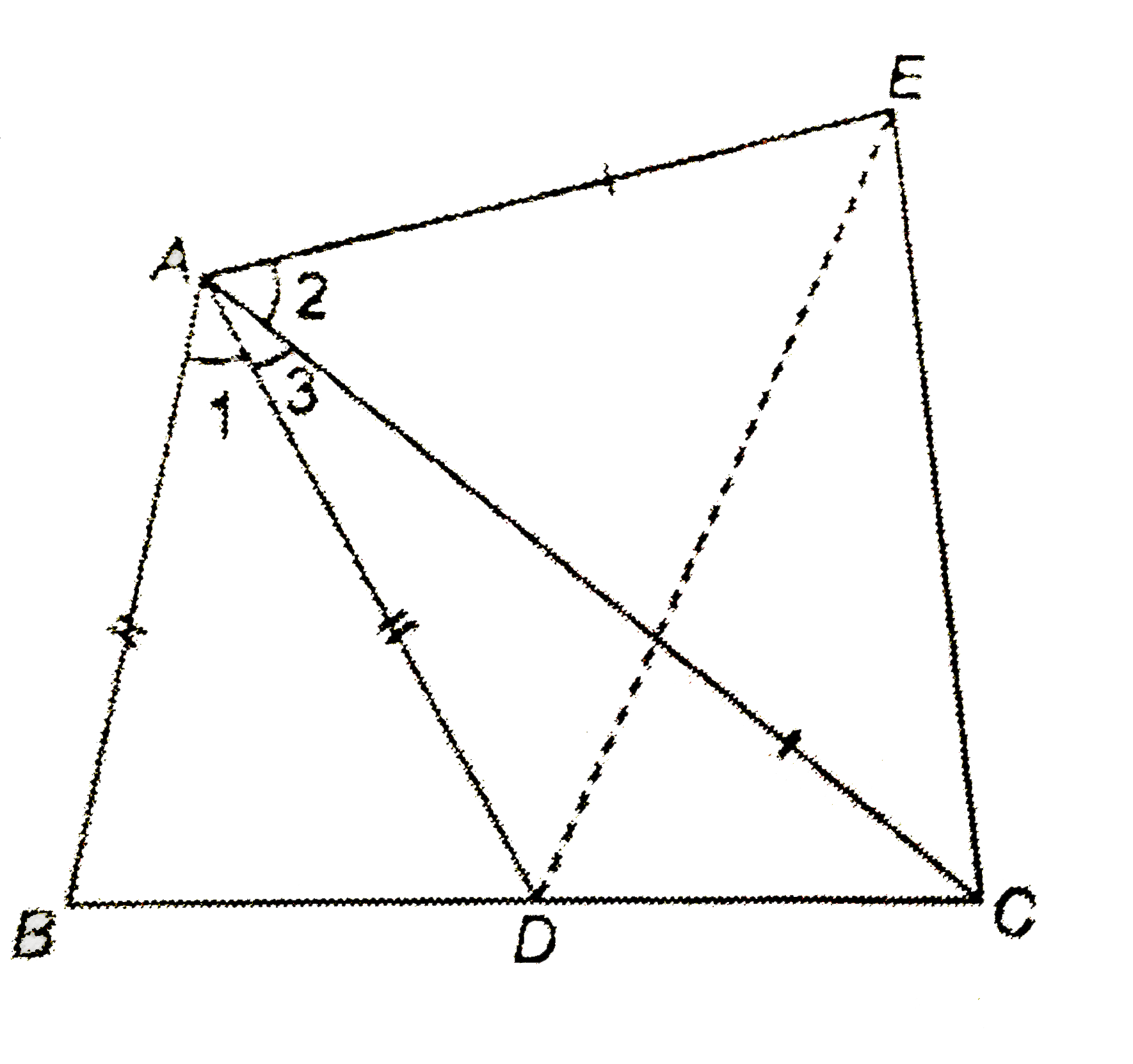
View SolutionIn Figure DEBC and CDEF. Prove that AD2=ABxAF.
View SolutionIn figure, DE || AC and DF || AE. Prove that BFFE=BEEC.
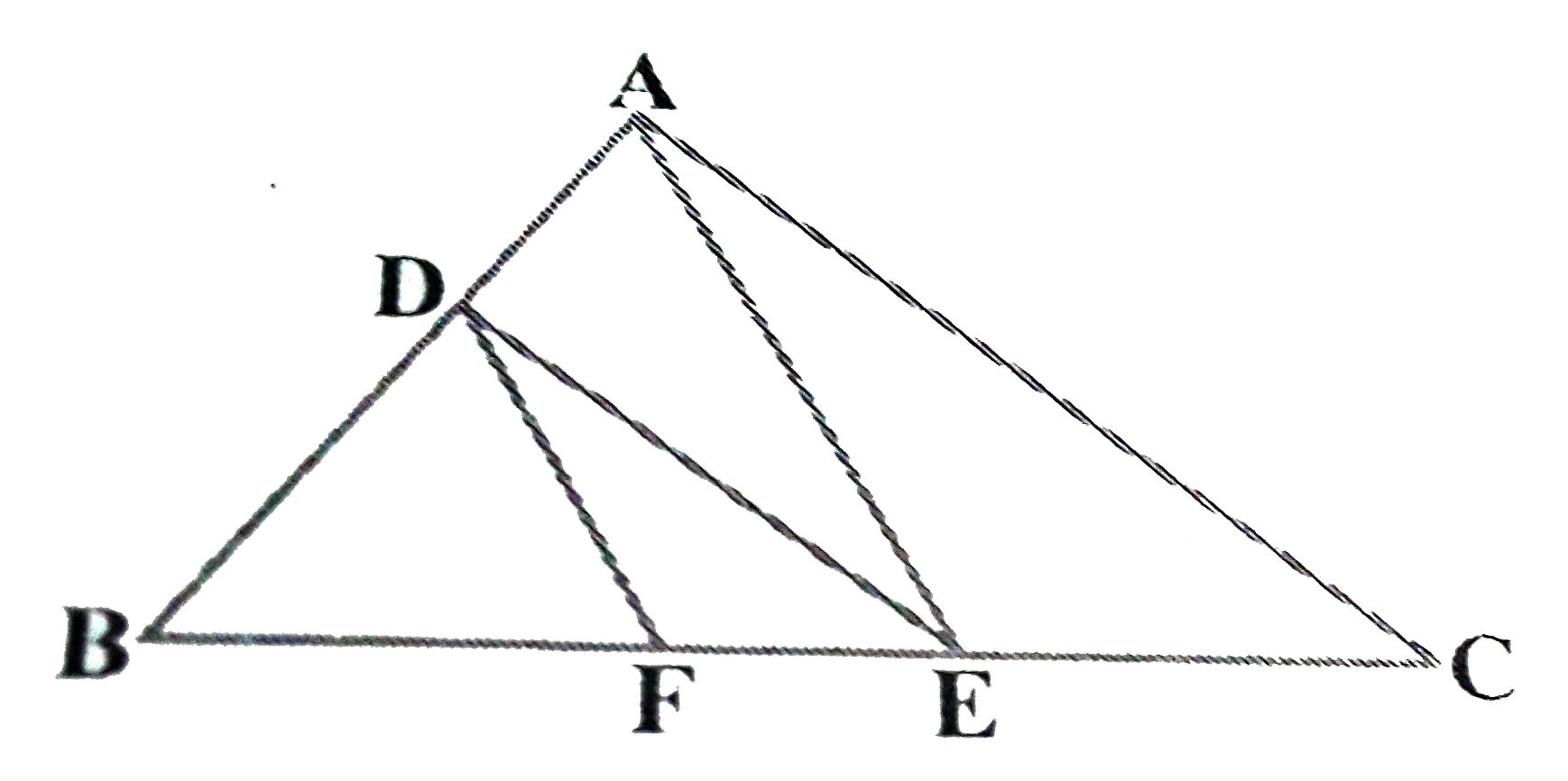
View SolutionIn the adjoining figure, AB=EF,BC=DE,∠ABC=∠FED=90∘, prove that AD=CF.
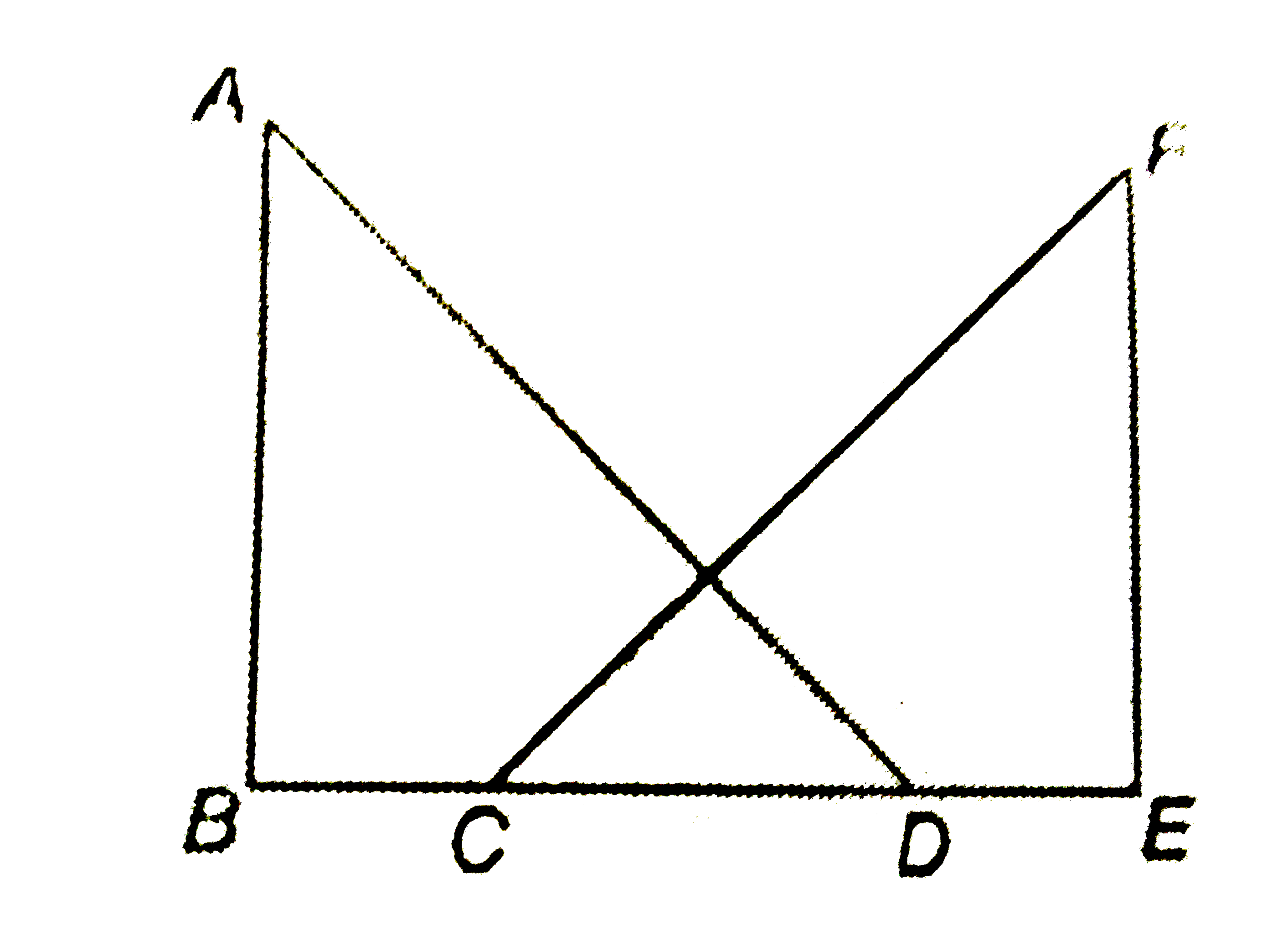
View SolutionIn the given figure DE || AC and BEEC=BCCP. Prove that DC || AP.
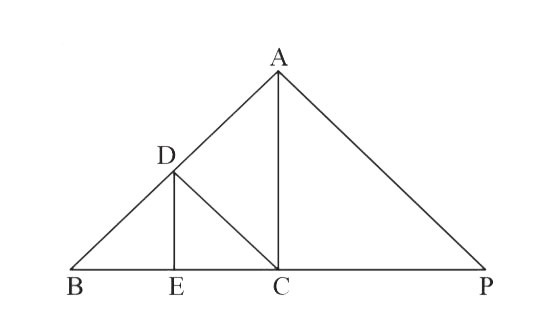
View SolutionIn Figure DEAC and DCap. Prove that BEEC=BCCP
View Solution