In figure, altitudes YZ and XT of △WXY intersect at P. Prove that
Points X,Z,T,Y are concyclic.
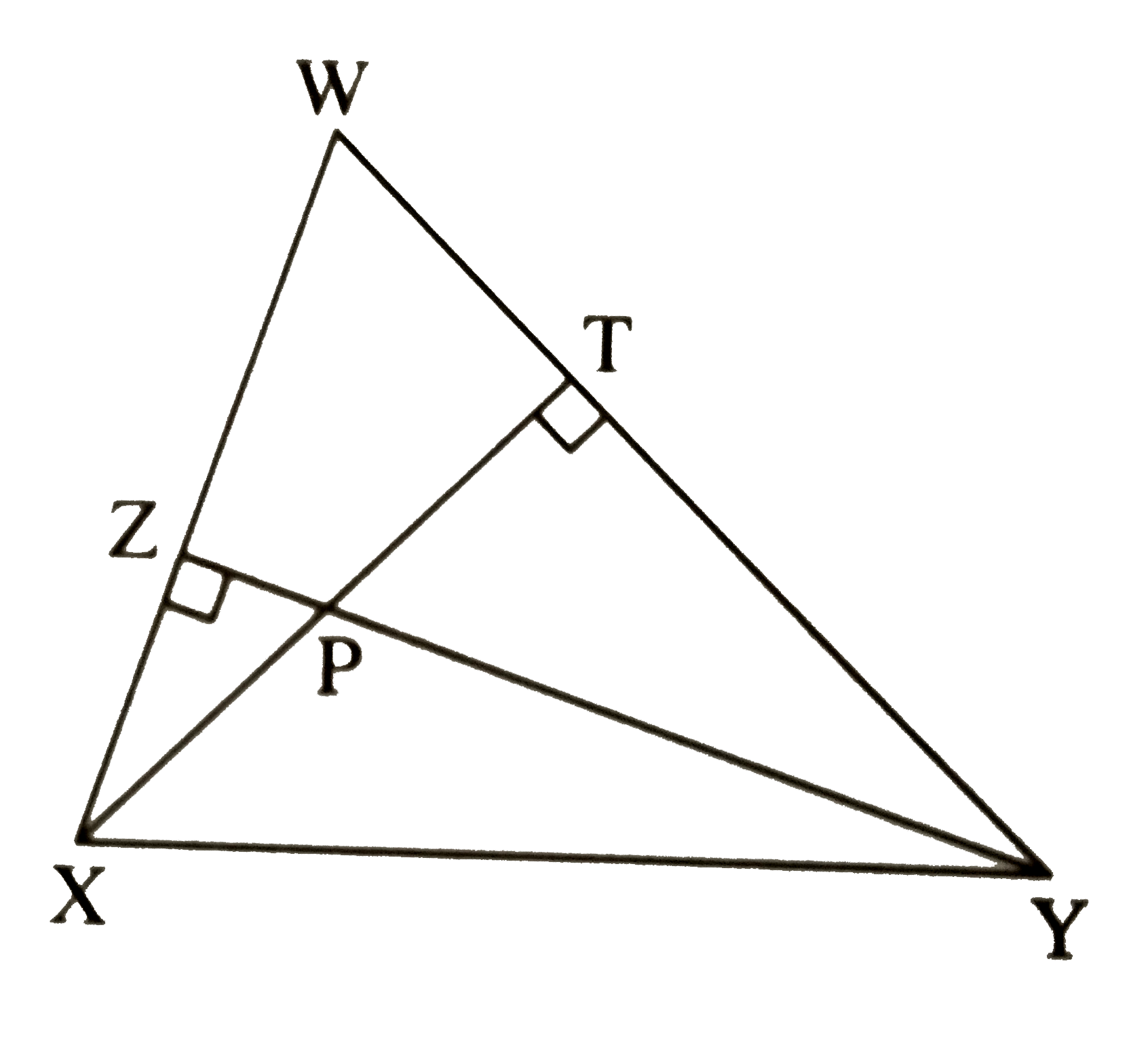
∠XZY=∠XTY=90∘ ………( Given )
∴ points X and Y on line XY subtend equal angles at two distinct points Z and T on the same side of line XY.
If two points on a given line subtend equal andles at two distinct points which le on the same side of the line, then the four points are concyclic. ltgtbrgt ∴ points X,Z,T,Y are concyclic.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.56videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PROBLEM SET 350videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.33videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :1videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.513videos
COORDINATE GEOMETRY
Similar Questions
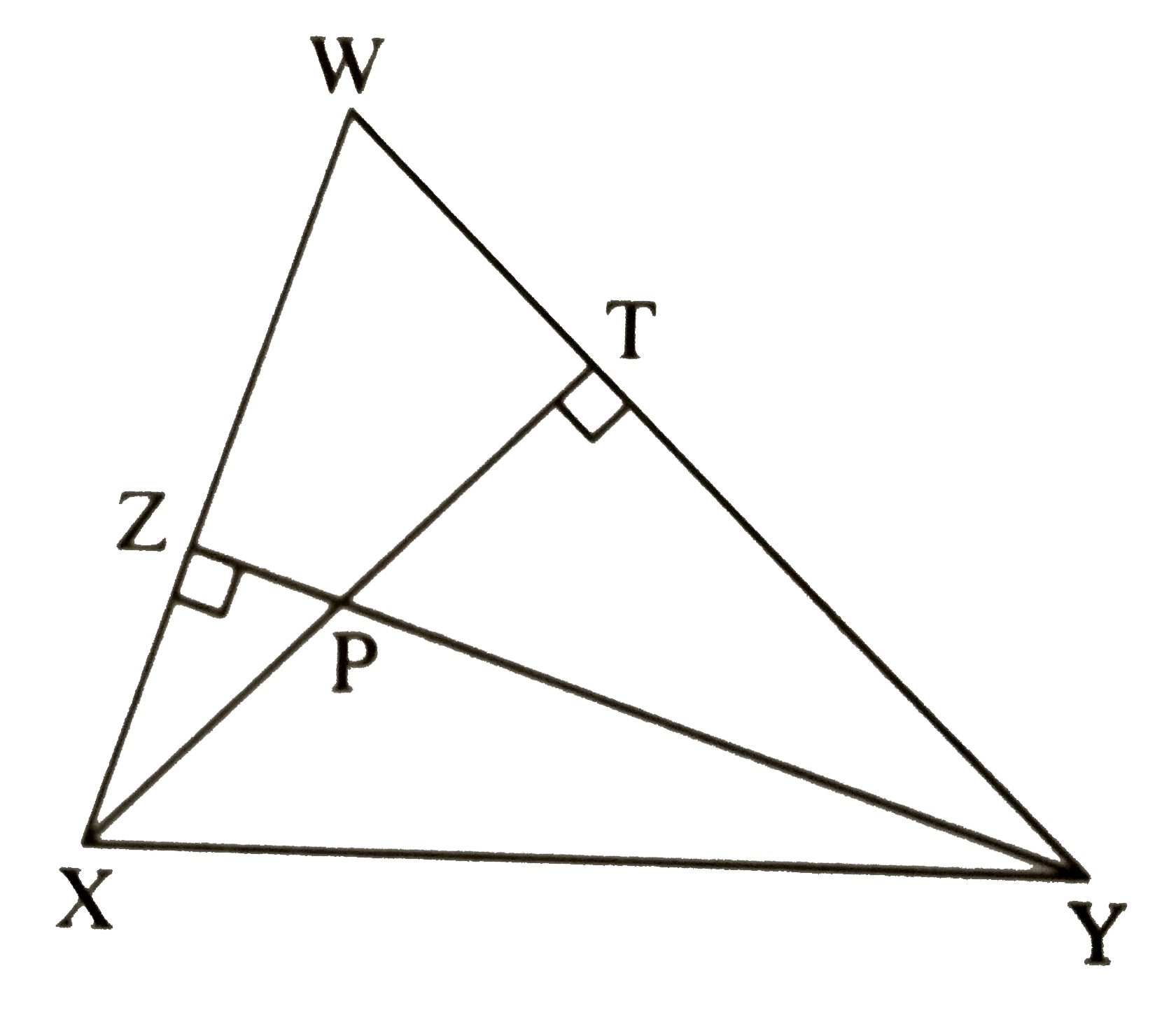
In figure, altitudes YZ and XT of △WXY intersect at P. Prove that
□WZPT is cyclic
 View Solution
View SolutionIf BM and CN are the perpendiculars drawn on the sides AC and BC of the ΔABC, prove that the points B, C, M and N are concyclic.
View SolutionIn the figure , altitudes AD and CE of ΔABC intersect each other at the point P . Show that :
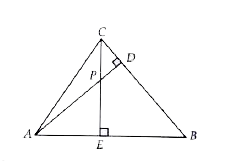
ΔAEP~ΔCDPView SolutionABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
View SolutionABC is an isosceles triangle in which AB=AC. If D and E are the mid-points of AB and AC respectively, prove that the points B, C, D and E are concyclic.
View SolutionA straight line through the vertex P of a triangle PQR intersects the side QR at the point S and the circuecirele of the triangle PQR at the point T. If S is not the centre of the circumeircle, then
View SolutionThe normal at three points P, Q, R on a rectangular hyperbola intersect at a point T on the curve. Prove that the centre of the hyperbola is the centroid of the triangle PQR.
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.
 View Solution
View SolutionTangents are drawn to the hyperbola 4x2−y2=36 at the points P and Q. If these tangents intersect at the point T(0,3) and the area (in sq units) of ΔTPQ is a√5 then a=
View SolutionIn the given figure, the two lines AB and CD intersect at a point O such that ∠BOC=125∘. Find the values of x, y, and z.
View Solution

