In figure, arcs have been drawn of radius 21 cm each with vertices A,B,C and D of quadrilateral ABCD as centres . Find the area of the shaded region.

Given that, radius of each arc ( r) = 21 cm
Arae of sector with ∠A=∠A360∘×πr2=∠A360∘×π×(21)2cm2 [∵ area of any sector with central angle θ and radius r = πr2360∘×θ]
Area of sector with ∠B=∠B360∘×πr2=∠B360∘×π×(21)2cm2
Area of sector with ∠C=∠C360∘×πr2=∠C360∘×π×(21)2cm2
and area of sector with ∠D=∠D360∘×πr2=∠D360∘×π×(21)2cm2
Therefore , sum of the areas (in cm2) of the four sectors
= ∠A360∘×π×(21)2+∠B360∘+π×(21)2+∠C360∘×π×(21)2+∠D360∘×π×(21)2
= (∠A+∠B+∠C+∠D)360∘×π×(21)2 [∴ sum of all interior angle in any quadrilaterl = 360∘]
= 22×3×21=1386cm2
Hence, required area of the shaded region is 1386cm2 .
Topper's Solved these Questions
- AREAS RELATED TO CIRCLEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - AREAS RELATED TO CIRCLEEXERCISE - Long Answer Type Questions
20 Videos
- AREAS RELATED TO CIRCLEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - AREAS RELATED TO CIRCLEEXERCISE - Very Short Answer Questions
14 Videos
- ARITHMETIC PROGRESSIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Long Answer Type Questions
10 Videos
Similar Questions
In figure arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region .

View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionIn Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
View SolutionIn Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
View SolutionIn figure, ABCD is a trapezium with AB|| DC . AB = 18 cm, DC = 32 cm and distance between AB and DC= 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.

View SolutionCombination of quadrilateral and circle : In Figure; ABCD is a trapezium with AB||DC ; AB = 18cm; DC = 32cm and the distance between AB and DC is 14 cm. Circles of Equal radii 7 cm with centres A;B;C and D have been drawn. Then; find the area of the shaded region of the figure.
View SolutionPQRS is a diameter of a circle of radius 6 cm. The length PQ, QR and RS are equal Semicircle are drawn on PQ and QS as diameters. Find the area of the shaded region. Find also the length of boundaries of shaded portion.
View SolutionIn Figure, ABC is an equilateral triangle inscribed in a circle of radius 4 cm with centre O . Find the area of the shaded region.
View SolutionIn figure, three sectors of a circle of radius 7 cm, making angles of 60∘,80∘ and 40∘ at the center are shaded. Find the area of the shaded region.
View Solution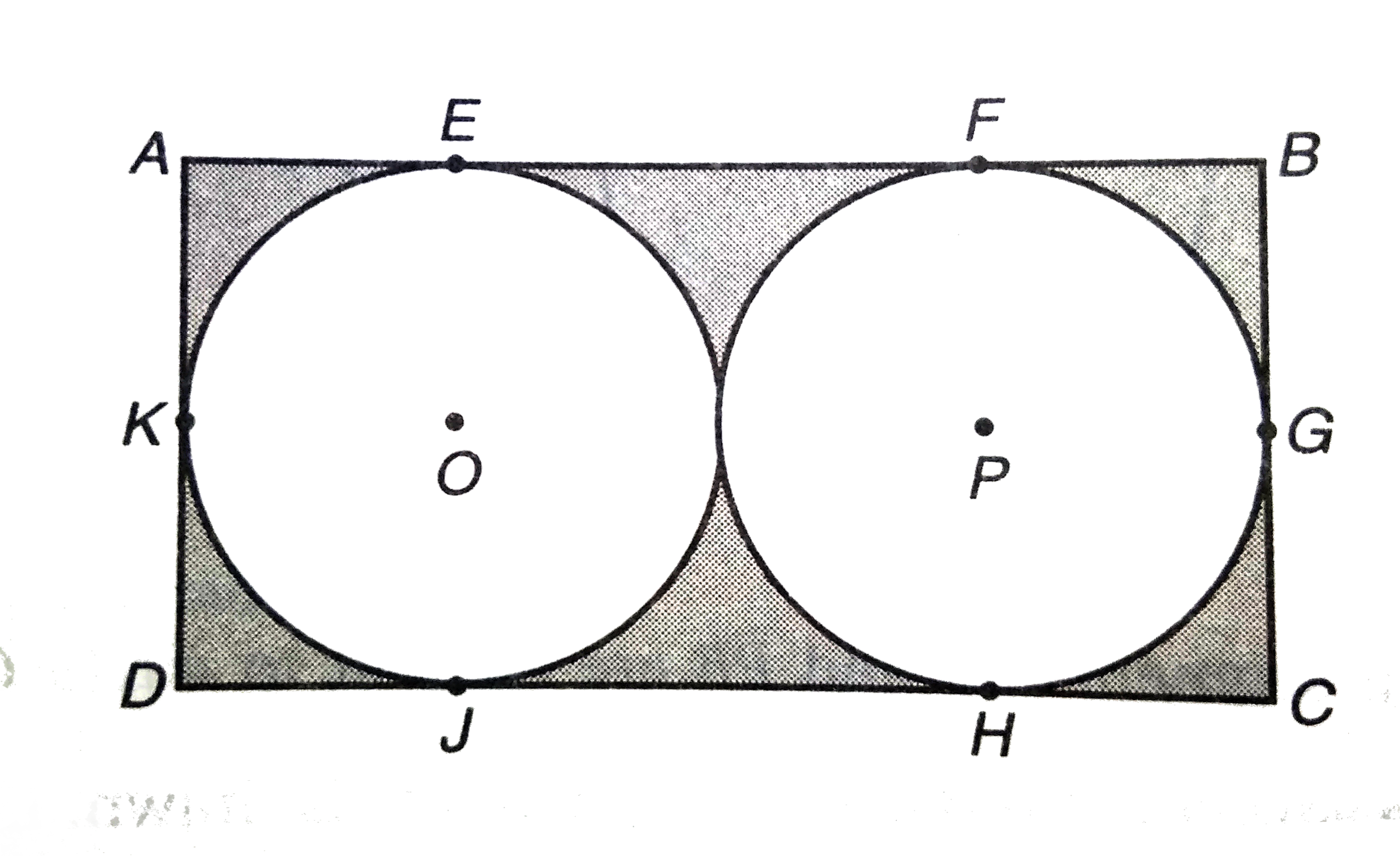
In the figure above, the radius of each circle is 1. If circles O and P touch the sides of rectangle ABCD only at the lettered points, what is the area of the shaded region?
View Solution
