In Figure, $∠ B A C = 90^{0}, A D$ is its bisector. If $D E ⊥ A c$ , prove that $D E x (A B + A C) = A B x A C$

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $= A B \times A C$ .

Answer

Step by step video, text & image solution for In Figure, /_B A C=90^0,A D is its bisector. If D E_|_A c , prove that D Ex(A B+A C)=A BxA C by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Subjective Problems) (Long Answer Type)
7 Videos
TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Integer Numerical Value Type)
10 Videos
TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Subjective Problems) (Very Short Answer Type)
10 Videos
SURFACE AREAS AND VOLUMESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos

Similar Questions

If $a < b$ and $c \leq d,$ prove that $a + c < b + d$
View Solution
In Fig. 4.124, $E$ is a point on side $C B$ produced of an isosceles triangle $A B C$ with $A B = A C$ . If $A D ⊥ B C$ and $E F ⊥ A C$ , prove that (i) $A B D E C F$ (ii) $A B \times E F = A D \times E C$ . (FIGURE)
View Solution
In figure $A B = A C a n d C P ∣ ∣ B A$ and $A P$ is the bisector of exterior $∠ C A D$ of $A B C$ . Prove that $∠ P A C = ∠ B C A$ (ii) $A B C P$ is a parallelogram
View Solution
In a $A B C$ , $A D$ is the bisector of $∠ A$ , meeting side $B C$ at $D$ . If $A B = 10 c m$ , $A C = 14 c m$ and $B C = 6 c m$ , find $B D$ and $D C$ (ii) If $A C = 4.2 c m$ , $D C = 6 c m$ and $B C = 10 c m$ , find $A B$ . (iii) If $A B = 5.6 c m$ , $A C = 6 c m$ and $D C = 3 c m$ , find $B C$ .
View Solution
In Figure, $A B C$ is an isosceles triangle in which $A B = A C . C P p a r e l \leq l A B$ and $A P$ is the bisector of exterior $∠ C A D$ of $A B C$ . Prove that $∠ P A C = ∠ B C A$ and (ii) $A B C P$ is a parallelogram.

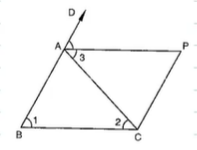
View Solution
In a parallelogram $A B C D,$ the bisector of $∠ A$ also bisects $B C$ at $X$ Prove that $A D = 2 A B$
View Solution
In figure, ABC is triangle in which $∠ A B C = 90^{\circ}$ and $A D ⊥ C B$ produced. Prove that $A C^{2} = A B^{2} + B C^{2} - 2 B C . B D$ .

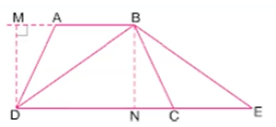
View Solution
In Figure, $A B C D$ is a trapezium in which $A B ∣ ∣ D C, D C$ is produced to $E$ such that $C E = A B,$ prove that $a r (A B D) = a r (B C E) .$ Construction: Draw $D M$ on $B A$ produced and $B N ⊥ D C$

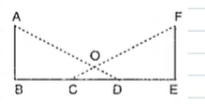
View Solution
In Figure, it is given that $A B = E F, B C = D E, A B ⊥ B D$ and $F E ⊥ C E .$ Prove that $A B D ≅ F E C .$

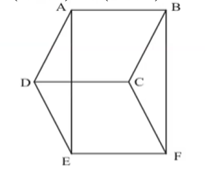
View Solution
In Figure, $A B C D, A B F E a n d C D E F$ are parallelograms. Prove that $a r (A D E) = a r (B C F)$

View Solution

MTG IIT JEE FOUNDATION-TRIANGLES - Exercise (Subjective Problems) (Short Answer Type)

P and Q are points on the sides AB and AC respectively of a triangleAB...
02:26
In A B C ,D is the mid-point of B Ca n dE D is the bisector of the /A...
04:41
In Figure, /B A C=90^0,A D is its bisector. If D E|A c , prove that D...
03:32
In given figure , OP = 5 cm and OR =12 cm and QR = 85 cm find the are...
02:23
In Fig. 4.123, ABCD is a trapezium with AB || DC. If Delta AED is sim...
03:28
In a triangleABC P and Q are points on AB and AC respectively and PQ||...
07:17
In figure , CD ||LA and DE||AC.find CL .
02:43
In an isoscles Delta ABC, AB= AC and D is a point on BC. Prove that AB...
05:10
In the figure given below, Delta PQR is right-angled at Q and the poin...
05:05
In trapezium ABCD. AB||DC and DC = 2AB. A line segment EF drawn parall...
03:31

Home
Ask Doubt
Profile

In Figure, ∠BAC=900,AD is its bisector. If DE⊥Ac , prove that DEx(AB+AC)=ABxAC

The correct Answer is:=AB×AC.

Topper's Solved these Questions

Similar Questions

MTG IIT JEE FOUNDATION-TRIANGLES - Exercise (Subjective Problems) (Short Answer Type)

In Figure, $∠ B A C = 90^{0}, A D$ is its bisector. If $D E ⊥ A c$ , prove that $D E x (A B + A C) = A B x A C$

The correct Answer is: $= A B \times A C$ .