In figure D is a point on side BC of a ΔABCsuch that BDCD=ABAC. Prove that AD is the bisector of ∠BAC.
GIVEN AΔABC in which D is point on BC such that BDDC=ABAC
TO PROVE AD is bisector of ∠A
CONSTRUCTION Produc BA to E such that BDDC=ABAC (give)
⇒BDDC=ABAE[∴AC=AE]
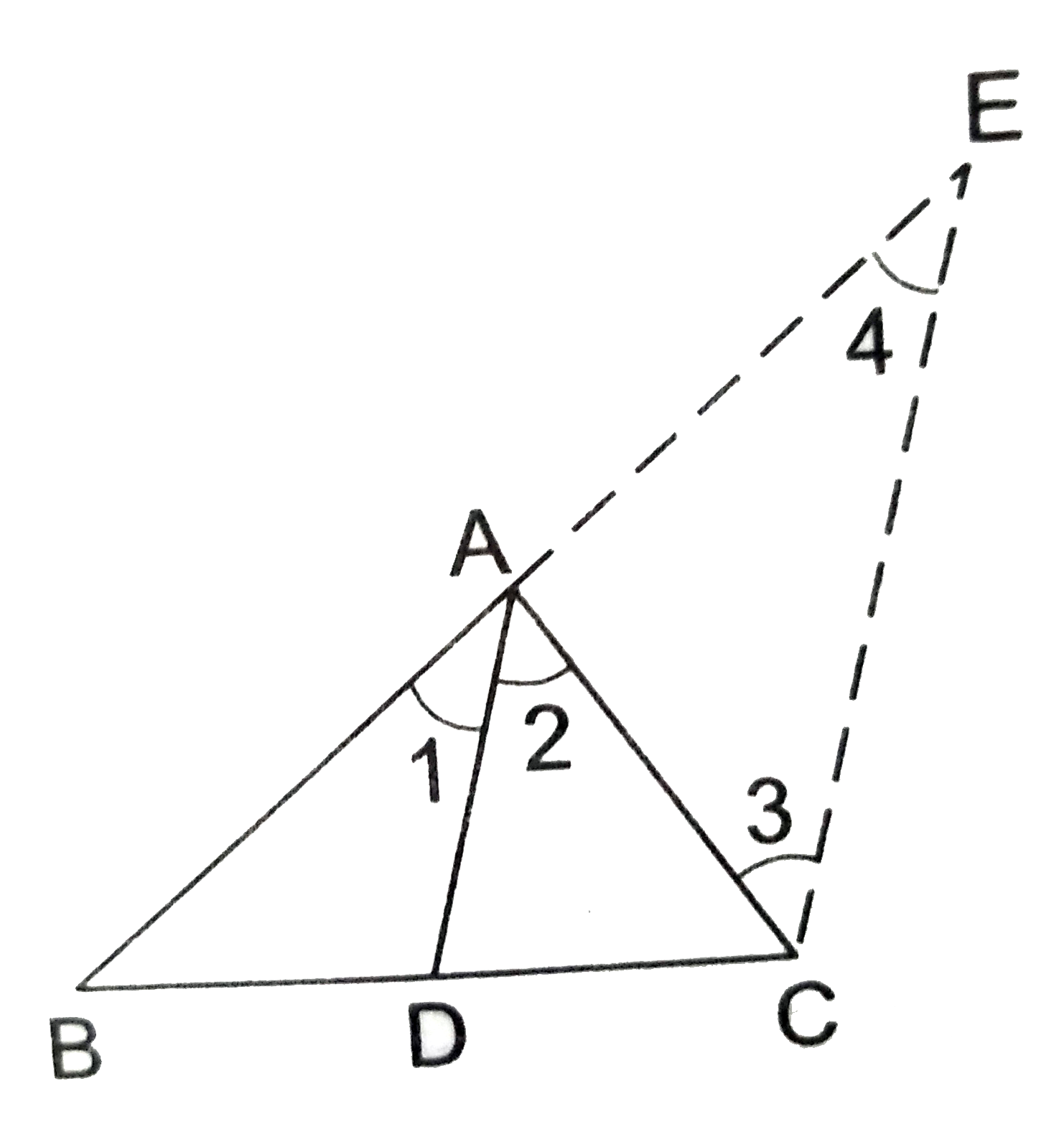
⇒DA∣∣CE [ by the converse of Thale's theorem]
∴∠2=∠3 ....(i). [ altervate int. ∠]
and ∠1=∠2 ...(ii) [ corresponding ∠]
Also, AE=AC⇒∠3=∠4 ...(iii)
∴∠1=∠2 [ from (i), (ii) and (iii)]
Hence, AD is the bisector of ∠A
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
In a scalene triangle ABC,D is a point on the side AB such that CD2=ADDB, sin s∈AS∈B=sin2C2 then prove that CD is internal bisector of ∠C.
View SolutionA point D is taken on the side BC of a ABC such that BD=2dC. Prove that ar(ABD)=2ar(ADC).
View SolutionD and E are points on sides AB and AC respectively of ΔABCsuch thatar (DBC) = ar (EBC). Prove that DE ∣∣ BC.
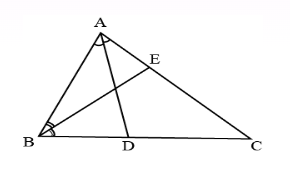
View SolutionIn Figure, ABC is a triangle in which ∠B=2∠C . D is a point on side BC such that AD bisects ∠BAC and AB=CD.BE is the bisector of ∠B . The measure of ∠BAC is
(a) 720
(b) 730
(c) 740
(d) 960
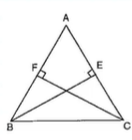
View SolutionIn Figure, BD and CE are two altitudes of a ABC such that BD=CE. Prove that ABC is isosceles.
View SolutionA point D is taken on the side BC of a ABC such that BD=2DC. Prove that ar ( ABD)= 2 ar ( ADC)
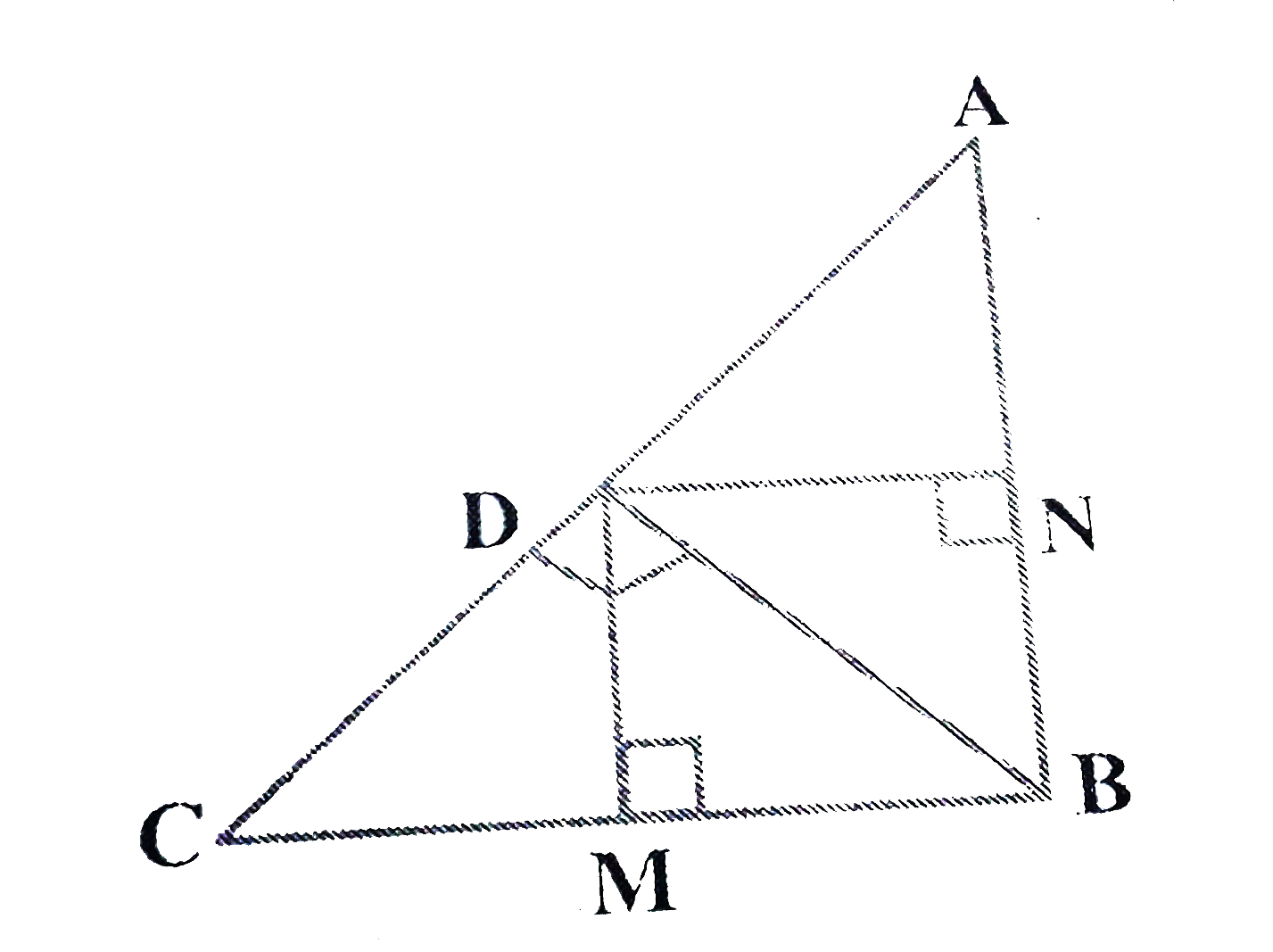
View SolutionIn fig., D is a point on hypotenuse AC of ΔABC,DM⊥BCand DN⊥AB. Prove that
(i) DM2=DN⋅MC
(ii) DN2=DM⋅AN
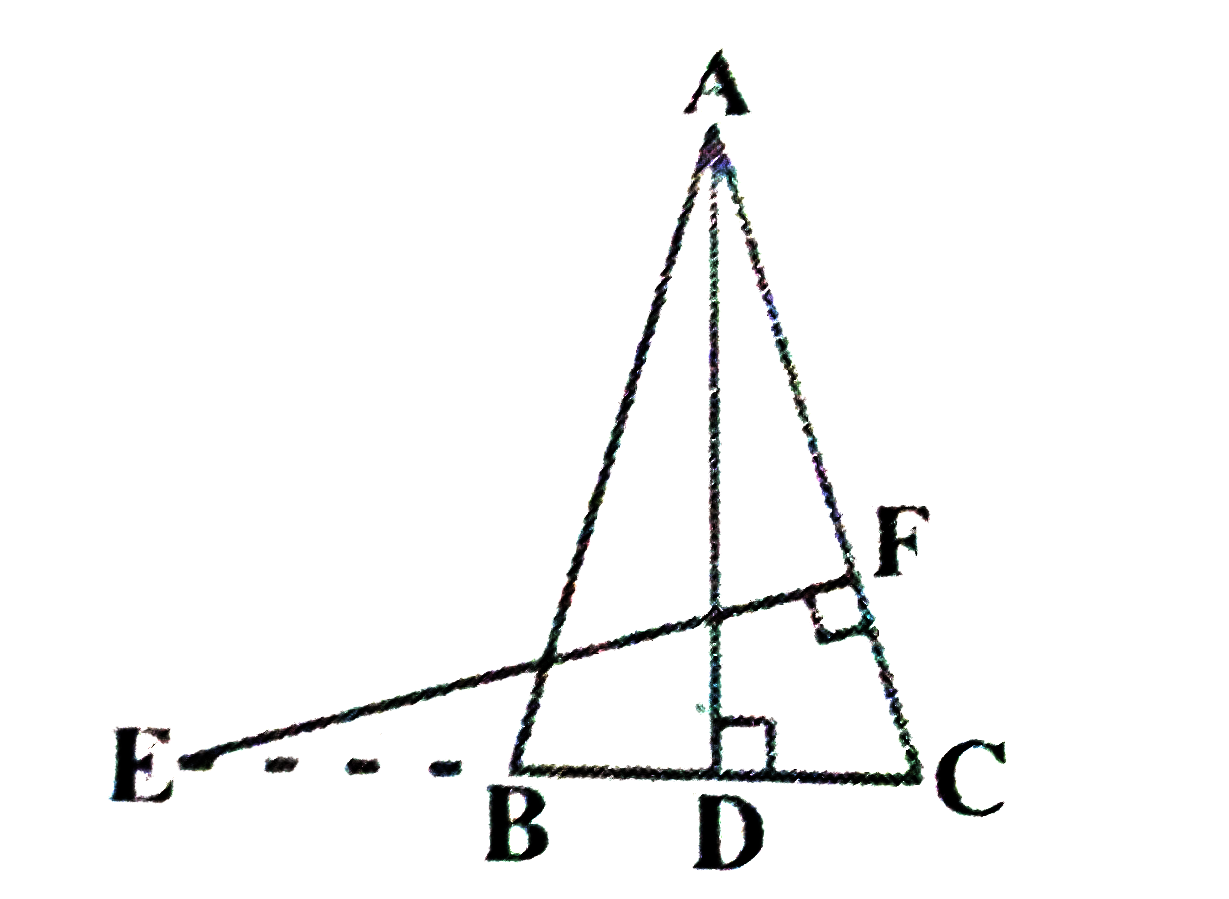
View SolutionIn figure E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD⊥BCandEF⊥AC, prove thatΔABD~ΔECF.
View SolutionIn figure, if ΔABE≅ΔACD, show that ΔADE~ΔABC.

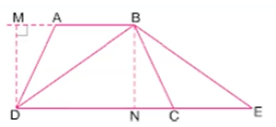
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣DC, DC is produced to E such that CE=AB, prove that ar(ABD)=ar (BCE). Construction: Draw DM on BA produced and BN⊥DC
View Solution