Question

A point ${\displaystyle D}$
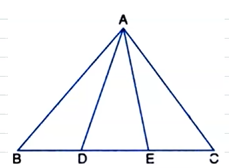
is taken on
the side ${\displaystyle BC}$
of a ${\displaystyle ABC}$
such that ${\displaystyle BD=2DC\stackrel{.}{}}$
Prove that ${\displaystyle ar ( ABD)= 2 ar ( ADC)}$

Explanation

To prove :
`ar(Δ ABD) = 2ar(Δ ADC)`
Proof : In `∆ABC`, we have


`BD = 2DC`


Let `E` be the midpoint of `BD` . Then ,


`BE = ED = DC`


Median of the triangle divides it into two equal triangles.


Since` AE` and `AD` are medians of `Δ's ABD` and `AEC`
.

∴ ar (ΔABD) = 2 ar (ΔAED) ……..(1)


and,


ar `(ΔADC) = ar (ΔAED)` ……..(2)



Now,


ar `(ΔABD) = 2 ar (ΔAED)`


ar `(ΔABD) = 2 ar (ΔADC)`

[From eq 2]


Hence, proved