In figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. Prove that AD = 2CD. 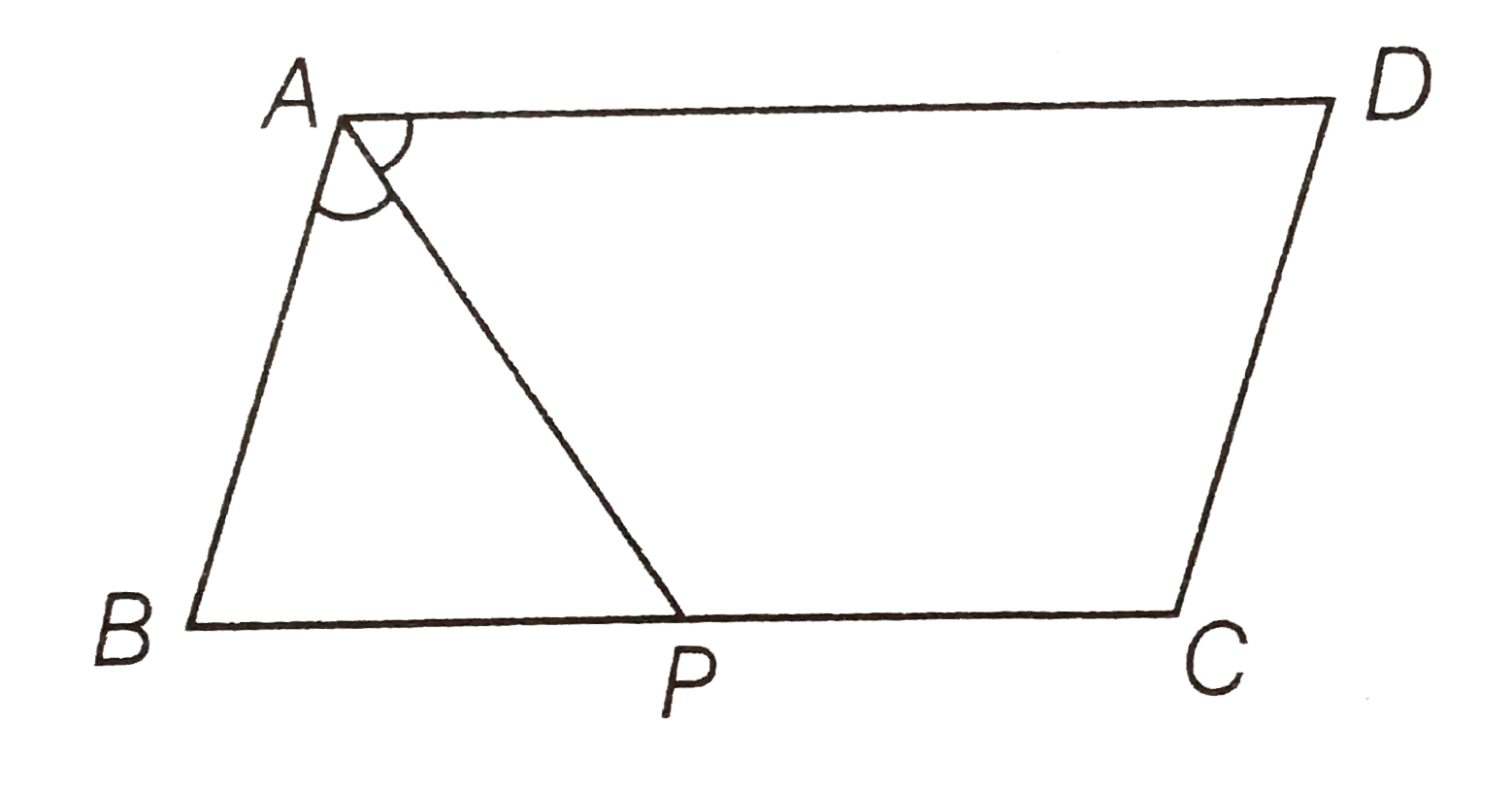
Given In a parallelogram ABCD, P is mid-point of BC such that ∠BAP=∠DAP.
To prove AD=2CD
Proof Since, ABCD is a parallelogram. ltBrgt So, AD∣∣BC and AB is transversal, then
∠A+∠B=180∘ [sum of cointerior angles is 180∘]
⇒ ∠B=180∘−∠A ...(i)
In ΔABP, ∠PAB+∠B+∠BPA=180∘ [by angle sum property of triangle]
⇒ 12∠A+180∘−∠A+∠BPA=180∘ [from Eq. (i)]
⇒ ∠BPA−∠A2=0
⇒ ∠BPA=∠A2 ...(ii)
⇒ ∠BPA=∠BAP
⇒ AB=BP [opposite sides of equal angles are equal]
On multiplying both sides by 2, we get
2AB=2BP
⇒ 2AB=BC [since P is the mid-point of BC] ltBrgt ⇒ 2CD=AD
[since, ABCD is a parallelogram, then AB=CD and BC =AD]
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRILATERALS EXERCISE - LONG ANSWER TYPE QUESTIONS18videos
QUADRILATERALS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRILATERALS EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS14videos
QUADRILATERALS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - POLYNOMIALSEXERCISE - EXERCISE 2.4 Long Answer type Questions9videos
POLYNOMIALS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS12videos
STATISTICS AND PROBABILITY
Similar Questions
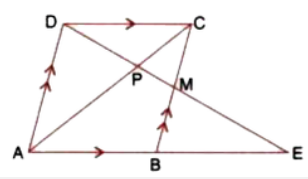
In the following figure, M is mid-point of BC of a parallelogram ABCD. DM intersects the diagonal AC at P and AB produced at E. Prove that : PE = 2 PD .
 View Solution
View SolutionE is the mid-point of side AB and F is the mid point of side DC of parallelogram ABCD . Prove that AEFD is a parallelogram.
View SolutionP is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
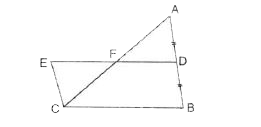
View SolutionIn the given figure, D is mid-point of side AB of △ABC and BDEC is a parallelogram.
Prove that :
Area of ΔABC = Area of //gmBDEC
 View Solution
View SolutionIf P and Q are the middle points of the sides BC and CD of the parallelogram ABCD, then AP+AQ is equal to
View SolutionP is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that :
DL:DP=AL:DCView SolutionE, F, G and H are the mid-points of the sides of a parallelogram ABCD. Show that area of quadrilateral EFGH is half of the area of parallelogram ABCD.
View SolutionIn the following figure, ABCD is a parallelogram. Prove that:

∠DAP+∠CBP=∠APBView SolutionIf E is a point on side AD produced of a parallelogram ABCD and BE intersects CD at F , Prove that △ABE~△CFB .
View SolutionX and Y are the mid-points of the opposite sides AB and DC of a parallelogram ABCD. Prove that □AXCY is a parallelogram.
View Solution
