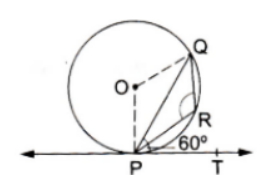
In Figure PQ is a chord of a circle with centre O and PT is a tangent. If QPT=60∘ so, find PRQ.
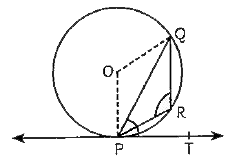
The correct Answer is:120∘
Step by step video, text & image solution for In Figure PQ is a chord of a circle with centre O and PT is a tangent. If QPT =60^@ so, find PRQ. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLESBOOK - EDUCART PUBLICATIONCHAPTER - CIRCLESEXERCISE - SHORT ANSWER (SA-I) Type Questions
28 Videos
- CIRCLESBOOK - EDUCART PUBLICATIONCHAPTER - CIRCLESEXERCISE - SHORT ANSWER (SA-II) Type Questions
18 Videos
- CIRCLESBOOK - EDUCART PUBLICATIONCHAPTER - CIRCLESEXERCISE - OBJECTIVE Type Questions (Write True or False)
8 Videos
- CBSE TERM-1 SAMPLE PAPER 2BOOK - EDUCART PUBLICATIONCHAPTER - CBSE TERM-1 SAMPLE PAPER 2EXERCISE - Section -C
7 Videos
- CONSTRUCTIONSBOOK - EDUCART PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - LONG ANSWER Type Questions
6 Videos
Similar Questions
Knowledge Check
In the given figure, AB is a chord of the circle with centre O and PQ is a tangent at point B of the circle. If ∠AOB=110∘, then ∠ ABQ is
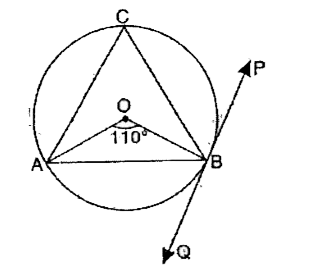 A45∘B70∘C55∘D35∘
A45∘B70∘C55∘D35∘In the figure , PQ is a chord of a circle and PT is a tangent at P such that ∠QPT=60∘, then ∠PRQ =
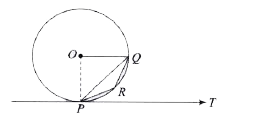 A100∘B110∘C120∘D150∘
A100∘B110∘C120∘D150∘In the figure below, AB is a chord of a circle with centre O. A tangent AT is drawn at point A so that ∠BAT=50∘. Then ∠ADB=?
 A120∘B130∘C140∘D150∘
A120∘B130∘C140∘D150∘
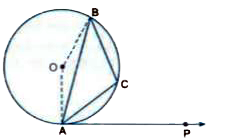
In fig AB is chord of a circle with centre O and AP is the tangent at A such that ∠BAP=75∘ find ∠ACB
View SolutionIn the adjoining figure, PQ is a chord of a circle and PT is the tangent at P such that ∠QPT=60∘.Find ∠PRQ.
View SolutionIn fig. PQ is a tangent to length 6cm to the circle with centre O and ∠OQP=60∘ . Find OQ

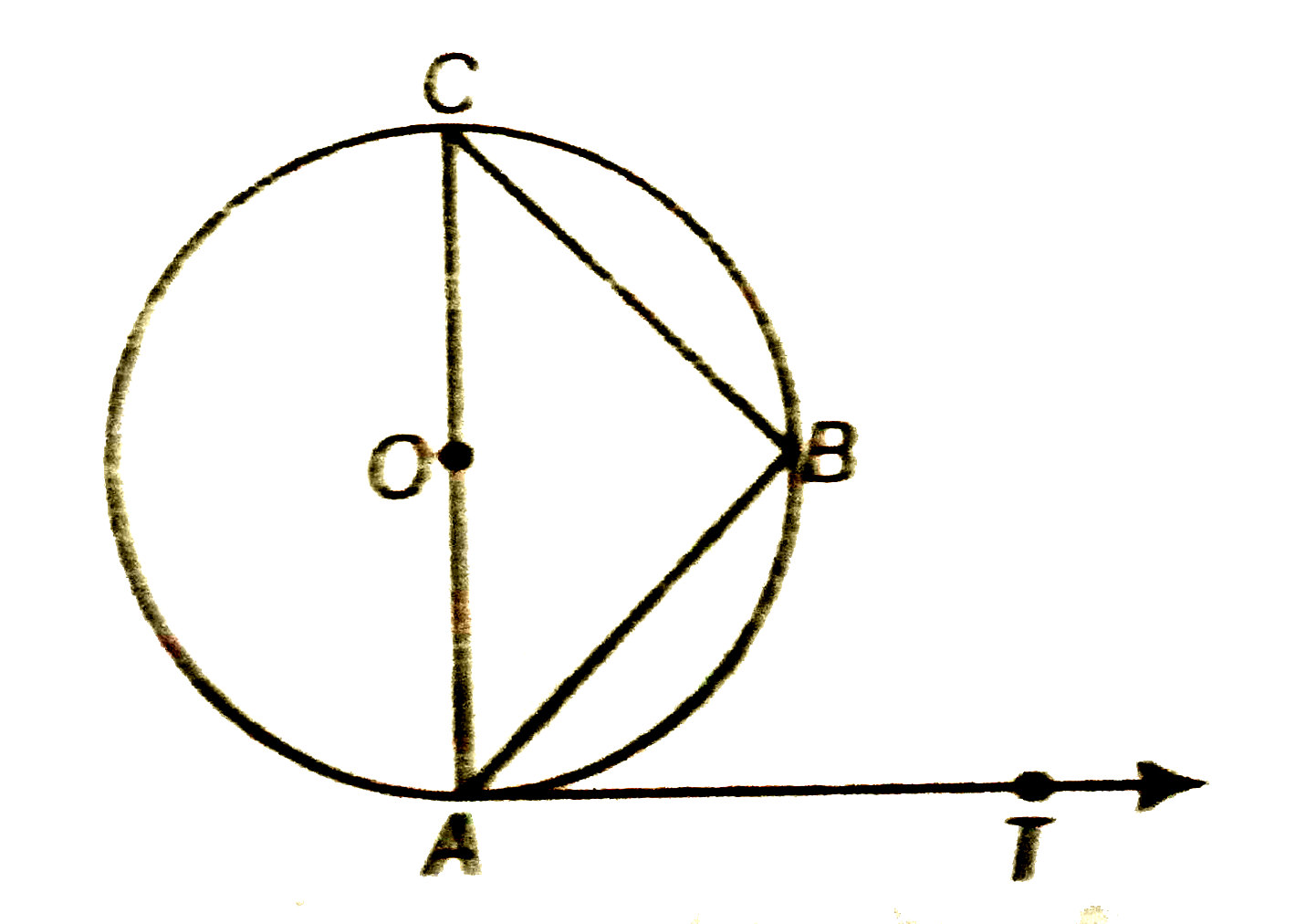
View SolutionIf AB is chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT=∠ACB.
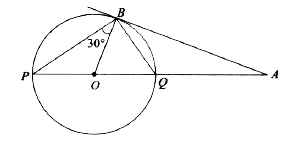
View SolutionIn the given figure , AB is a tangent to the circle with centre O and ∠BPQ=40∘ . Find PQ : AQ.
View Solution
