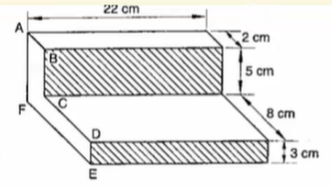
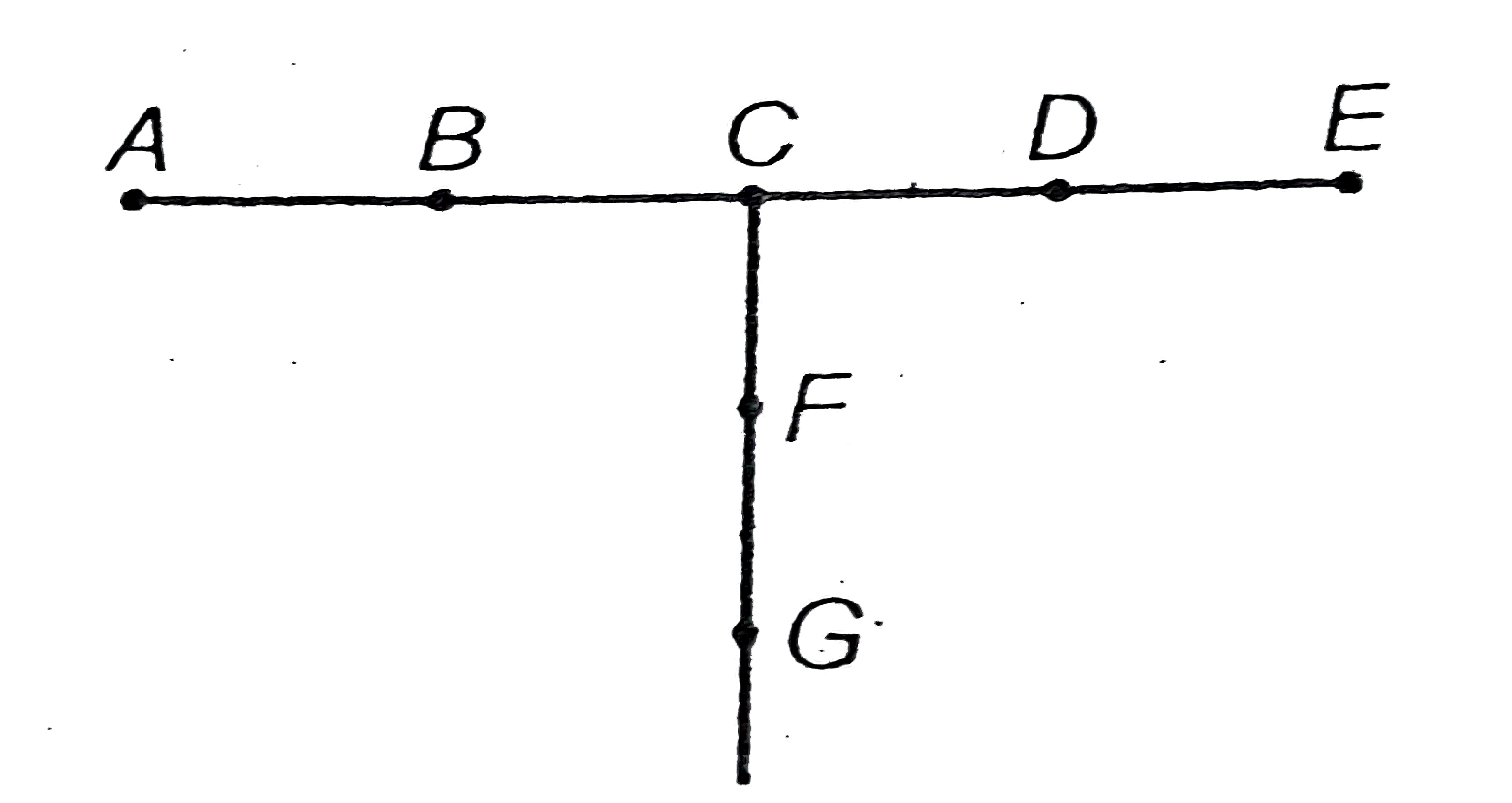
In Figure,
the shape of a solid copper piece (made of two pieces with dimensions as
shown in the figure) is shown. The face ABCDEFA
is the
uniform cross-section. Assume that the angles at A, B, C, D and F
are right
angles. Calculate the volume of the piece.
Step by step video & image solution for In Figure, the shape of a solid copper piece (made of two pieces with dimensions as shown in the figure) is shown. The face A B C D E F A is the uniform cross-section. Assume that the angles at A ,\ B ,\ C ,\ D\ a n d\ F are right angles. Calculate the volume of the piece. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Figure, the shape of a solid copper piece (made of two pieces with dimensions as shown in the figure) is shown. The face ABCDEFA is the uniform cross-section. Assume that the angles at A, B, C, D and F are right angles. Calculate the volume of the piece.
View SolutionIn figure, the the A the shows shape of a solid copper piece (made of two pieces) with dimensions is shown. The face ABCDEF is the uniform cross-section. Assume that, the angles right angles. at A, B, C, D, E and F are Calculate the volume of the piece.
View SolutionIn Figure, find the four angles A, B, C and D in the parallelogram ABCD

View SolutionExamine the figures A, B, C, D, E and F. In which one of the four options all the items, A, B, C, D, E and Fare correct?
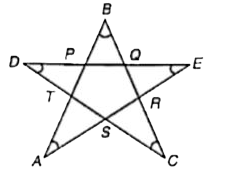
View SolutionIn the adjoining figure, a star is shown. What is the sum of the angles A, B, C, D and E?
View SolutionCalculate the area of the pentagon ABCDE , where AB=AE and with dimensions as shown in Fig.36.
View SolutionFrom the given figures identify the A,B,C,D,E and F
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ

View SolutionThe number of different triangles formed by joining the points A,B,C,D,E,FandG as shown in the figure given below is
View SolutionThe number of different circles passing through the points A,B,C,D,E,F and G as shown in the adjacent figure.
View Solution
