The number of different circles passing through the points A,B,C,D,E,F and G as shown in the adjacent figure.
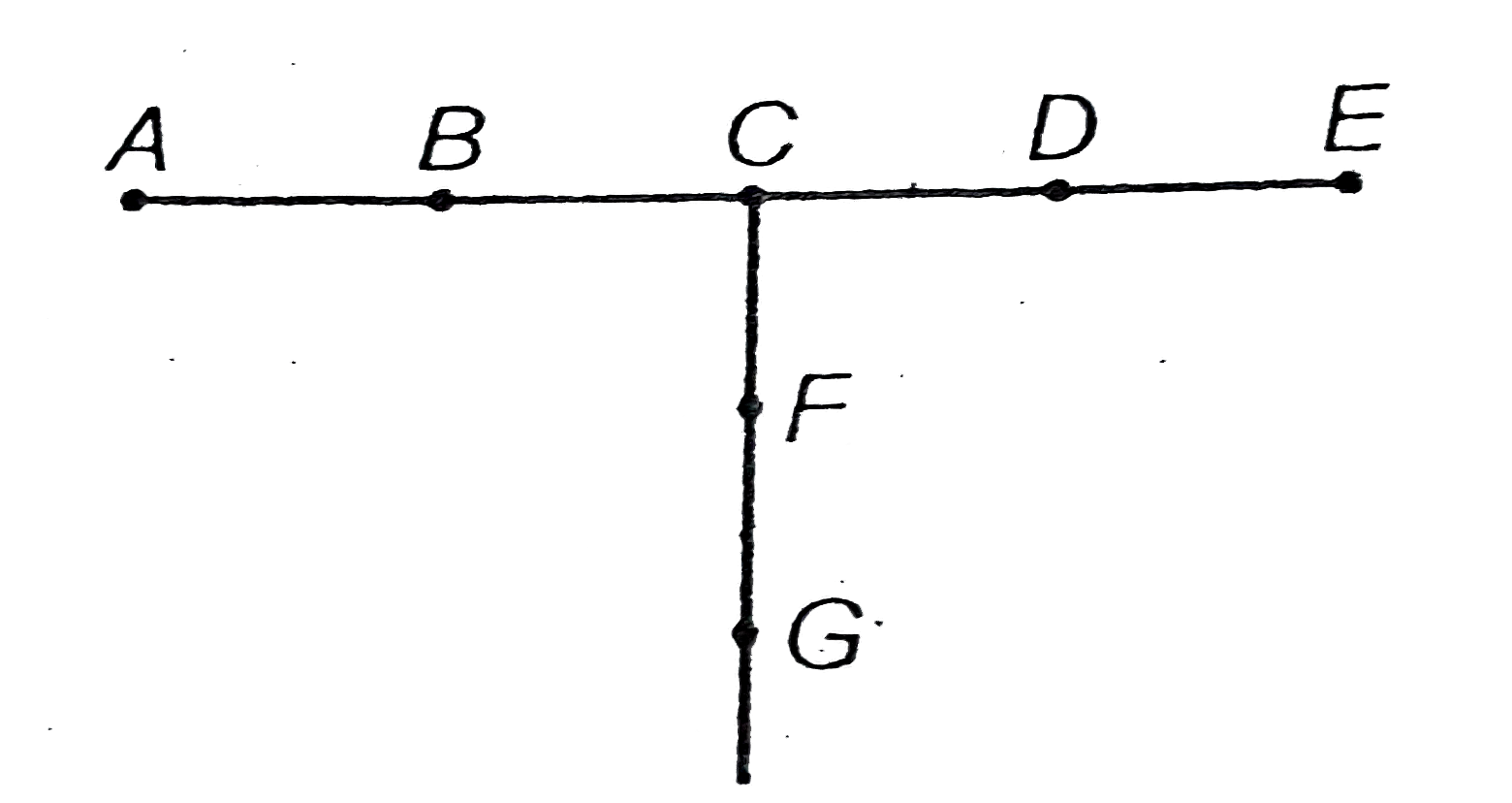
We know that from three non-collinear points one and only one circle can be drawn.
Hence, the number of different circles.
=Number of 3 non-collinear points selected from the given figure
=5C2×2C1+4C1×2C2
=20+4=24
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONS Book:AAKASH INSTITUTEChapter:PERMUTATIONS AND COMBINATIONS Exercise:Try Yourself
Explore 65 Videos
- PERMUTATIONS AND COMBINATIONS Book:AAKASH INSTITUTEChapter:PERMUTATIONS AND COMBINATIONS Exercise:Assignment Section A Objective type questions (One option is correct )
Explore 51 Videos
- MATRICESBook:AAKASH INSTITUTEChapter:MATRICESExercise:Assignment (Section - J) Aakash Challengers Questions
Explore 3 Videos
- PRINCIPLE OF MATHEMATICAL Book:AAKASH INSTITUTEChapter:PRINCIPLE OF MATHEMATICAL Exercise:Section-D:(Assertion-Reason Type Questions)
Explore 12 Videos
Similar Questions
The number of different triangles formed by joining the points A,B,C,D,E,FandG as shown in the figure given below is
View SolutionA circle passes through A,B,C and D as shown in the figure. If ∠BAD=63∘, find x.
View SolutionWrite down the co-ordinates of each points A,B,C,D,E and F as shown in following figure.
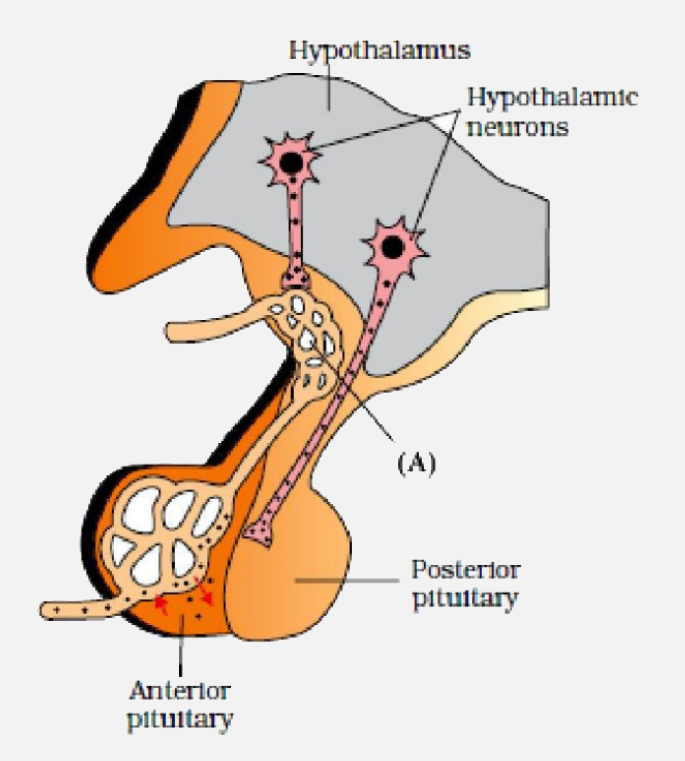
View SolutionWhich of the followig hormones passes through "route-A" shown in the adjacent figure?
View Solution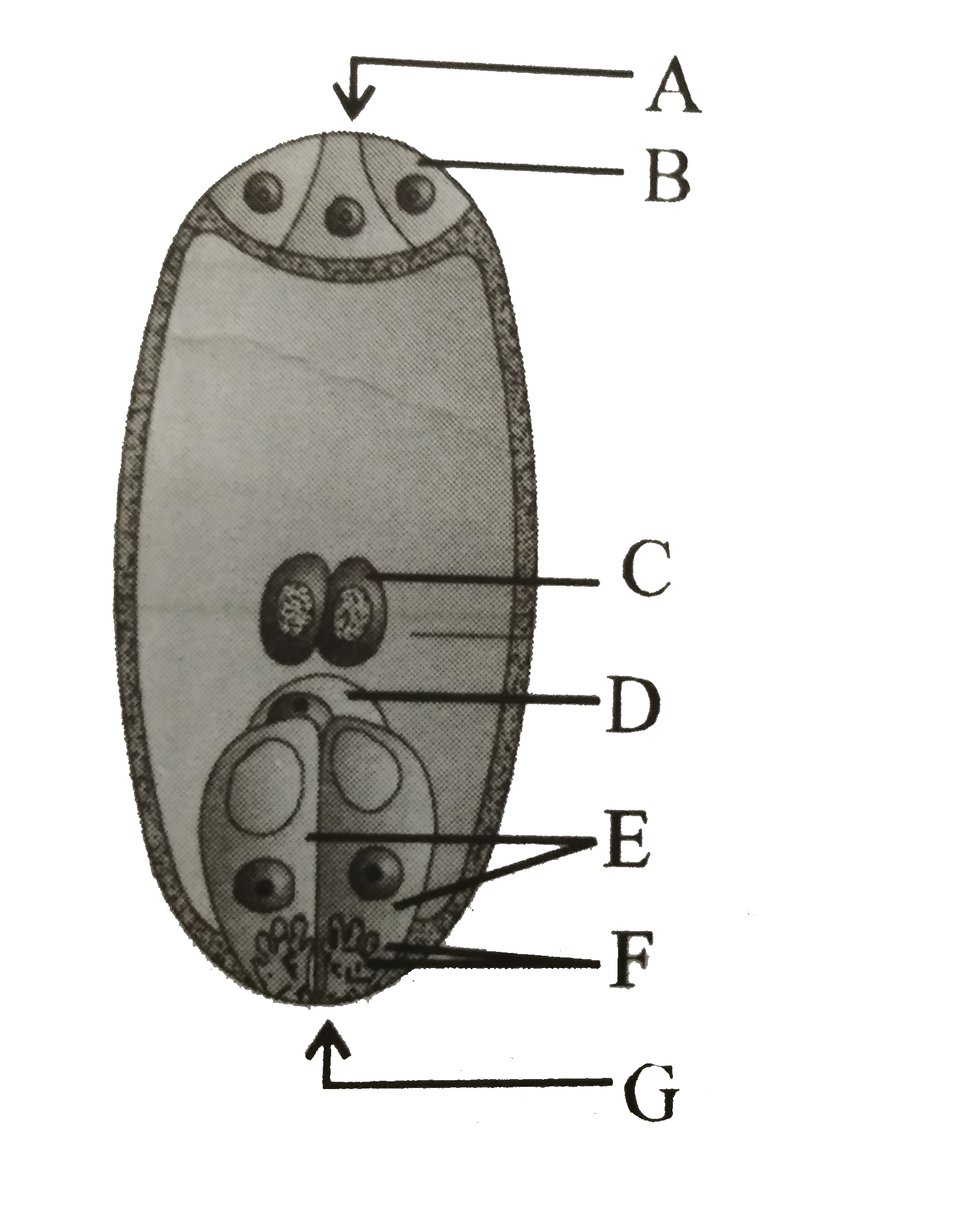
Identify A, B, C, D, E, F,G
View SolutionThere are 10 points in a plane of which no three points are collinear and four points are concyclic. The number of different circles that can be drawn through at least three points of these points is (A) 116 (B) 120 (C) 117 (D) none of these
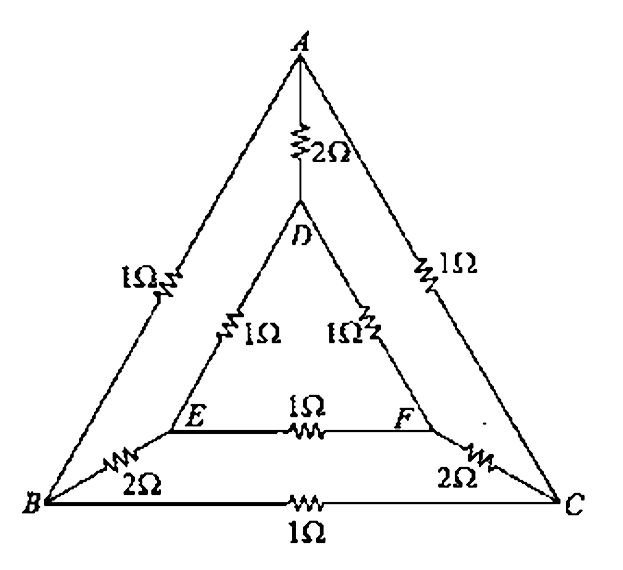
View SolutionA network of nine conductors connects six points A,B , C,D,E and F as shown in figure -3.97. The figure denotes resistances in ohms. Find the equivalents resistance between A and D.
[1Ω]
View Solution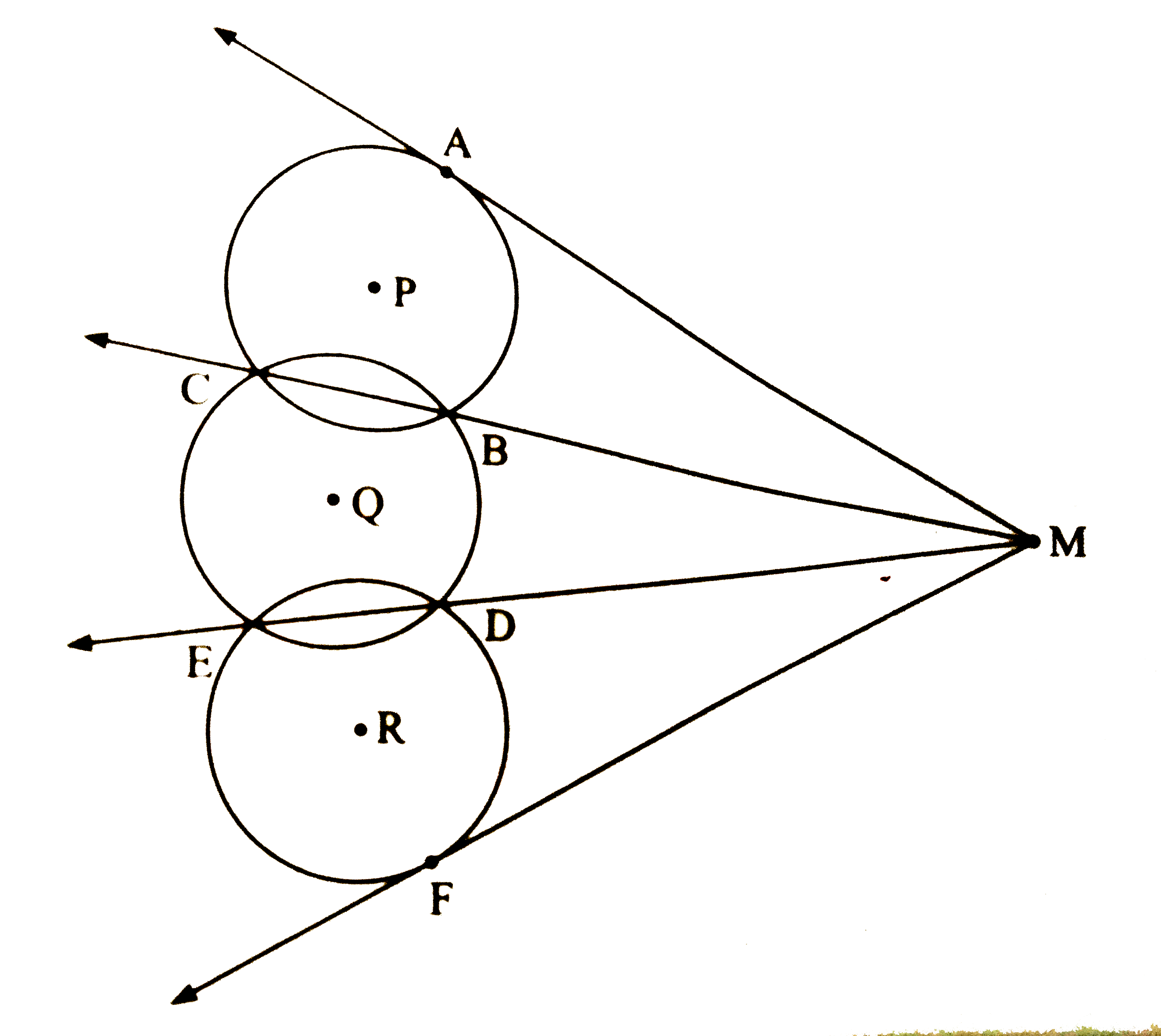
In the above figure,the circles with centres P,Q and R intersect at point B,C,D and E as shown. Lines CB and ED intersect in point M. Lines drawn from point M touch the circles at points A and F. Prove that MA = MF.
View SolutionThere are five points A,B,C,D and E. no three points are collinear and no four are concyclic. If the line AB intersects of the circles drawn through the five points. The number of points of intersection on the line apart from A and B is
View SolutionIn Figure, ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EFDC
View Solution
