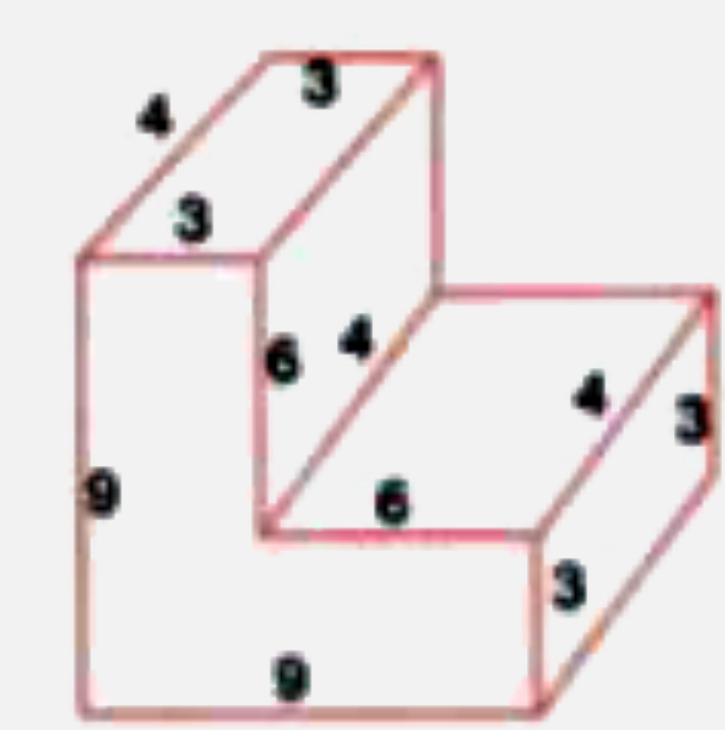
In Figure, the shape of a solid copper piece (made of two pieces with dimensions as shown in the figure) is shown. The face ABCDEFA is the uniform cross-section. Assume that the angles at A, B, C, D and F are right angles. Calculate the volume of the piece.
To calculate the volume of the solid copper piece made of two cuboids, we will follow these steps:
Step 1: Identify the dimensions of the upper cuboid
- The length (AG) of the upper cuboid is given as 22 cm.
- The breadth (GH) of the upper cuboid is given as 2 cm.
- The height (HI) of the upper cuboid is given as 5 cm.
Step 2: Calculate the volume of the upper cuboid
The formula for the volume of a cuboid is:
Volume=Length×Breadth×Height
Substituting the values:
Volumeupper=22cm×2cm×5cm
Volumeupper=220cm3
Step 3: Identify the dimensions of the lower cuboid
- The length (FE) of the lower cuboid can be calculated as:
Length=FM+ME=2cm+8cm=10cm
- The breadth (DJ) of the lower cuboid is the same as AG, which is 22 cm.
- The height (JK) of the lower cuboid is given as 3 cm.
Step 4: Calculate the volume of the lower cuboid
Using the same volume formula:
Volumelower=Length×Breadth×Height
Substituting the values:
Volumelower=10cm×22cm×3cm
Volumelower=660cm3
Step 5: Calculate the total volume of the copper piece
To find the total volume, we add the volumes of the upper and lower cuboids:
Total Volume=Volumeupper+Volumelower
Total Volume=220cm3+660cm3
Total Volume=880cm3
Final Answer
The volume of the solid copper piece is 880cm3.
---
- The length (AG) of the upper cuboid is given as 22 cm.
- The breadth (GH) of the upper cuboid is given as 2 cm.
- The height (HI) of the upper cuboid is given as 5 cm.
The formula for the volume of a cuboid is:
Volume=Length×Breadth×Height
Substituting the values:
Volumeupper=22cm×2cm×5cm
Volumeupper=220cm3
- The length (FE) of the lower cuboid can be calculated as:
Length=FM+ME=2cm+8cm=10cm
- The breadth (DJ) of the lower cuboid is the same as AG, which is 22 cm.
- The height (JK) of the lower cuboid is given as 3 cm.
Using the same volume formula:
Volumelower=Length×Breadth×Height
Substituting the values:
Volumelower=10cm×22cm×3cm
Volumelower=660cm3
To find the total volume, we add the volumes of the upper and lower cuboids:
Total Volume=Volumeupper+Volumelower
Total Volume=220cm3+660cm3
Total Volume=880cm3
The volume of the solid copper piece is 880cm3.
Topper's Solved these Questions
Similar Questions
In Figure, find the four angles A, B, C and D in the parallelogram ABCD
View SolutionCalculate the area of the pentagon ABCDE , where AB=AE and with dimensions as shown in Fig.36.
View SolutionFrom the given figures identify the A,B,C,D,E and F
View SolutionIn Figure, lines AB, CD and EF intersect at O. Find the measures of ∠AOC, ∠COF, ∠DOE and ∠BOF .
View SolutionIn Figure, lines l1and L2 intersect at O , forming angles as shown in the figure. If a=350, find the values of b, c and d.
View SolutionIn Figure ABCD and AEFD are two parallelograms. Prove that: PE=FQ
View SolutionThe following figure shows a solid of uniform cross-section. Find the volume of the solid. All measurements are in centimetres. Assume that all angles in the figure are right angles.
View SolutionThe following figure shows a solid of uniform cross-section. Find the volume of the solid.
All measurements are in centimetres. Assume that all angles in the figure are right angles.
View SolutionIn Figure, ABCD and AEFG are parallelograms. If ∠C=550, what is the measure of ∠F?
View SolutionIn two congruent triangles ABC and DEF, if AB=DE and BC=EF. Name the pairs of equal angles.
View Solution
