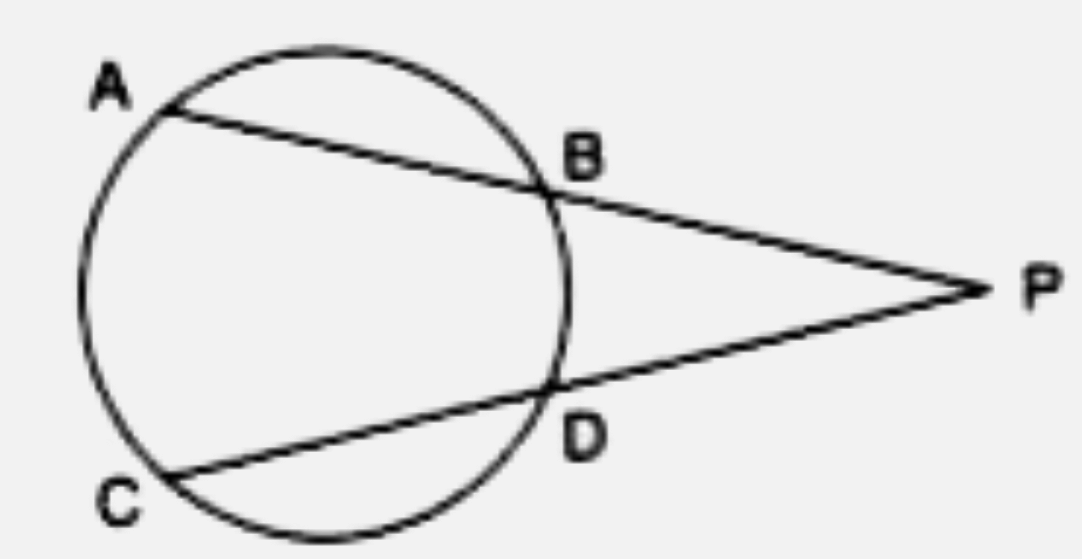
In Figure two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC~ΔPDB
(ii) PA⋅PB = PC⋅PD

(i) In △PAC and △PDB,
∠BAC=180∘−∠PAC (linear pairs)
∠PDB=∠CDB=180−∠BAC
=180∘−(180∘−∠PAC)=∠PAC
∠PAC=∠PDB ... (1)
∠APC=∠BPD [Common] ... (2)
We know that in a cyclic quadrilateral, the exterior angle is equal to the interior opposite angle.
Therefore, for cyclic quadrilateral ABCD.
consider ABCD , ΔPAC and ΔPBD.
∠PCA=∠PBD .... (3)
∴ By AAA-criterion of similarity,
△PAC∼△DPB (proved)
(ii) △PAC∼△DPB
So, the corresponding sides of the similar triangles are proportional
PAPD=PCPD
⇒PA.PB=PC.PD
(proved)
Topper's Solved these Questions
Similar Questions
Two equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.

Prove that:
BP=DP
View SolutionThe equal chords AB and CD of circle with centre O, when produced, meet at P outside the circle. Prove that :
PB=PD
View SolutionThe equal chords AB and CD of circle with centre O, when produced, meet at P outside the circle. Prove that :

PA=PC.
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionIn Figure, two chords AB and CD intersect each other at the point P. Prove that:
(i) ΔAPC~ΔDPB
(ii) AP⋅PB=CP⋅DP

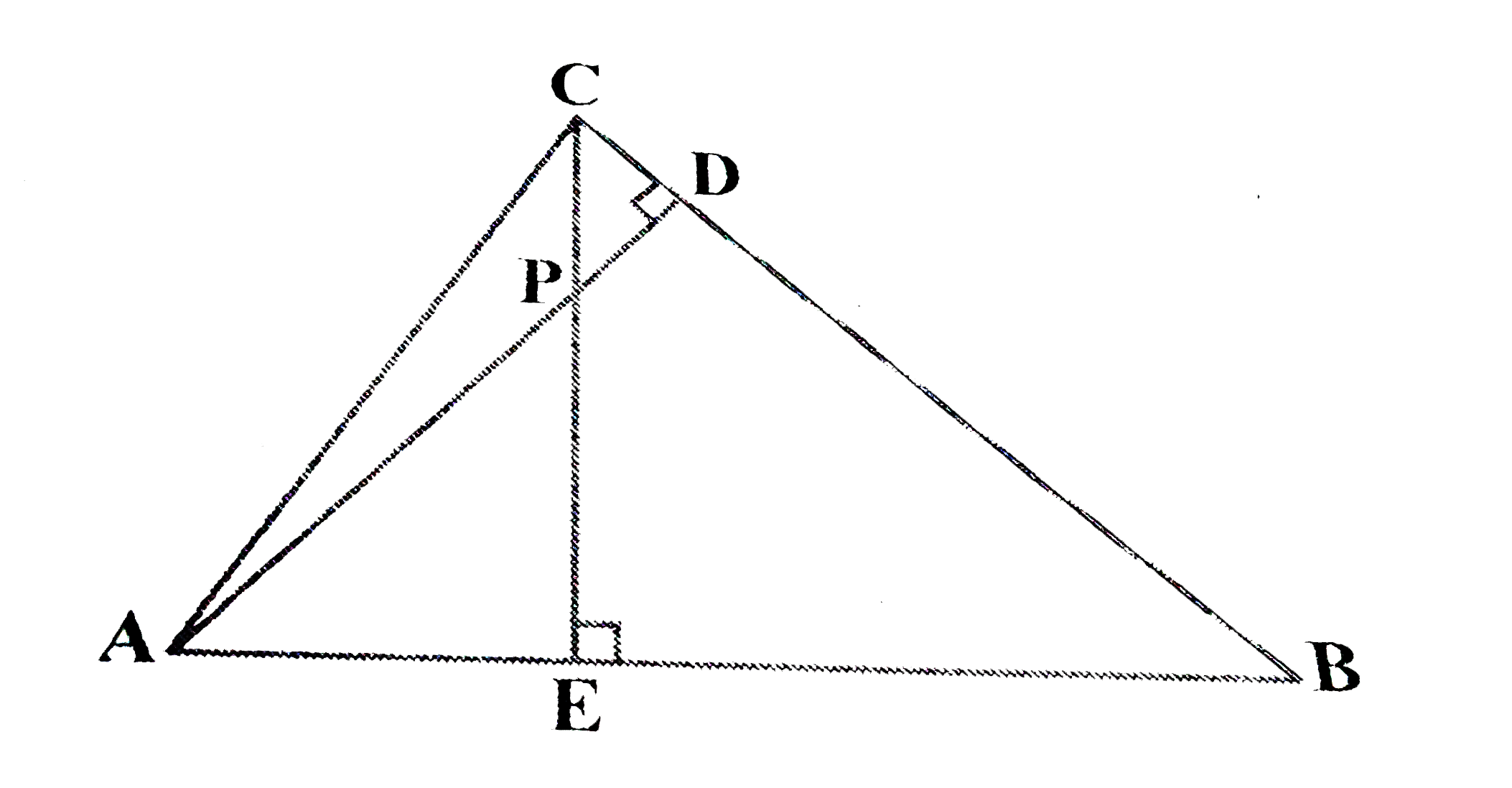
View SolutionIn Figure altitudes AD and CE of A B C intersect each other at the point P. Show that:(i) ΔAEP~ΔCDP (ii) ΔABD~ΔCBE (iii) ΔAEP~ΔADB(iv) ΔPDC~ΔBEC
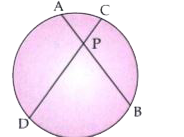
View SolutionAB and CD are two chords of a circle intersecting at P. Prove that AP×PB=CP×PD
View SolutionAB and CD are two chords of a circle intersecting at a point P outside the circle. If
PC=30cm, CD=14cm and PA=24cm, determine AB.
View SolutionAB and CD are two chords of a circle intersecting at a point P outside the circle. If
PA= 8cm, PC= 5cm and PD= 4cm, determine AB.
View SolutionIn Figure, AB and CD are two chords of a circle, intersecting each other at P such that AP=CP. Show that AB=CD.
View Solution
