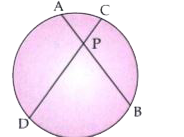
In Figure, two chords AB and CD intersect each other at the point P. Prove that:
(i) ΔAPC~ΔDPB
(ii) AP⋅PB=CP⋅DP

(i) In the given figure,
∠APC=∠DPB --> as opposite angles between two lines are equal
∠CAB=∠CDB --> as angle subtended by an arc are always equal on any point of circle
It means, ∠CAP=∠PDB
In ΔAPC and ΔDPB
∠APC=∠DPB
∠CAB=∠CDB
Thus, by Angle-Angle Similarity rule,
ΔAPC ~ ΔDPB
(ii) ΔAPC ~ ΔDPB
APDP=CPPB
Hence,AP.PB=CP.DP
Similar Questions
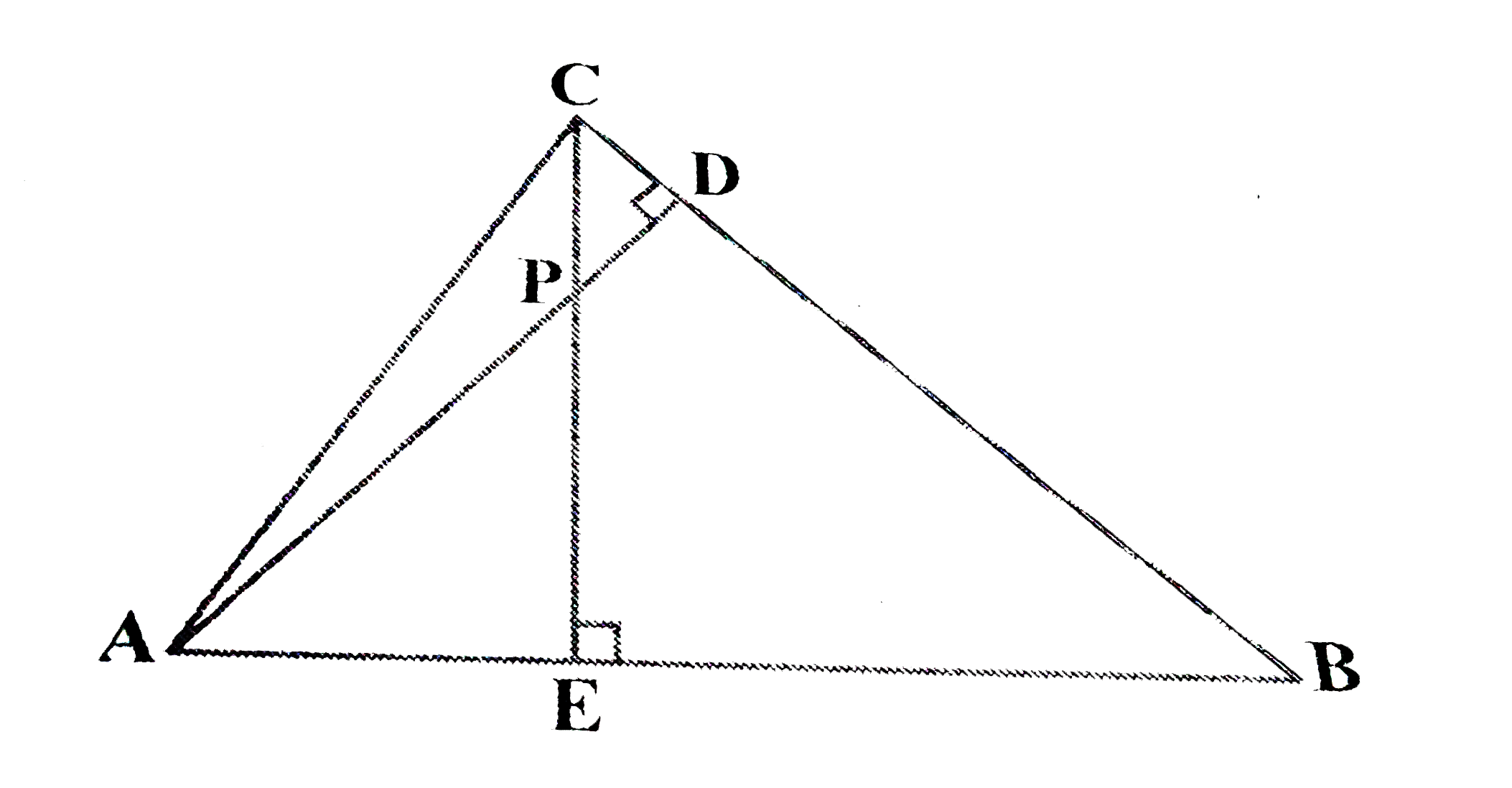
In Figure altitudes AD and CE of A B C intersect each other at the point P. Show that:(i) ΔAEP~ΔCDP (ii) ΔABD~ΔCBE (iii) ΔAEP~ΔADB(iv) ΔPDC~ΔBEC
View SolutionIn Figure two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC~ΔPDB
(ii) PA⋅PB = PC⋅PD

View SolutionTwo equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.

Prove that:
BP=DP
View SolutionIn Figure, AB and CD are two chords of a circle, intersecting each other at P such that AP=CP. Show that AB=CD.
View SolutionIn figure ABC and AMP are two right triangles, right angles at B and M respectively. Prove that(i) ΔABC~ΔAMP (ii) CAPA=BCMP

View SolutionIn Figure, P, is any point on the chord BC of a circle such that AB=AP. Prove that CP=CQ.
View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ. Show that:
(i) ΔAPD≅ΔCQB
(ii) AP=CQ
(iii) ΔAQB≅ΔCPD
(iv) AQ=CP
(v) APCQ is a parallelogram.

View SolutionAB and CD are two chords of a circle intersecting at P. Prove that AP×PB=CP×PD
View SolutionTwo circles with centres A and B intersect each other at points P and Q. Prove that the centre-line AB bisects the common chord PQ perpendicularly.
View SolutionIn Figure, ABCD and PQRC are rectangles and Q is the mid-point of AC . Prove that DP=PC (ii) PR=12 AC
View Solution
