In Figure, X,Y
are the mid-points of opposite sides AB
and DC
of a parallelogram ABCD.AY
and DX
are joined intersecting inP;CX
and BY
are joined intersecting in Q.
Show that
DXBY is a parallelogram,
PXQY
is parallelogram.
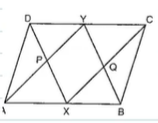
Step by step video & image solution for In Figure, X ,Y are the mid-points of opposite sides A B and D C of a parallelogram A B C DdotA Y and D X are joined intersecting inP ; C X and B Y are joined intersecting in Qdot Show that DXBY is a parallelogram, P X Q Y is parallelogram. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
In Figure, X, Y are the mid-points of opposite sides AB and DC of a parallelogram ABCD.AY and DX are joined intersecting in P;CX and BY are joined intersecting in Q . Show that AXCY is a parallelogram (ii) DXBY is a parallelogram quadrilateral PXQY is a parallelogram
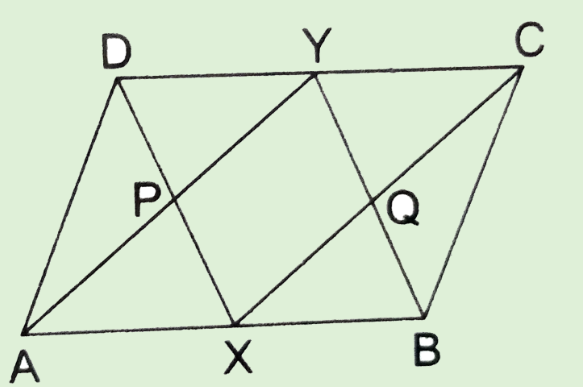 View Solution
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View Solution
Knowledge Check
- Question 1 - Select One
X and Y are the mid-points of the opposite sides AB and DC of a parallelogram ABCD. Then □AXCY is a ?
ATrapeziumBKiteCRhombusDParallelogram
In Figure, ABCD is a parallelogram and X,Y are the mid=points of sides AB and DC respectively. Show that AXCY is a parallelogram.
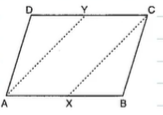 View Solution
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionE,F,G,H are respectively, the mid-points of the sides AB,BC,CD and DA of parallelogram ABCD . Show that the quadrilateral EFGH is a parallelogram and that its area is half the area of the parallelogram, ABCD. GIVEN : A quadrilateral ABCD in which L,F,G,H are respectively the mid-points of the sides AB,BC,CD and DA. TO PROVE : (i) Quadrilateral EFGH is a parallelogram ar(^(gm)EFGH)=12ar(^(gm)ABCD) CONSTRUCTION : Join AC and HF
View SolutionThe figure formed by joining the mid-points of the adjacent sides of a quadrilateral is a parallelogram (b) rectangle square (d) rhombus
View SolutionShow that the segment joining the mid-points of a pair of opposite sides of a parallelogram, divides it into two equal parallelograms.
View SolutionThe figure formed by joining the mid-point of the adjacent sides of a parallelogram is a rectangle (b) parallelogram (c) rhombus (d) square
View SolutionThe diagonals of a parallelogram ABCD intersect at OA line through O intersects AB at XandDC at Y Prove that OX=OY
View Solution

