Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Video Solution
Text Solution
Proof:
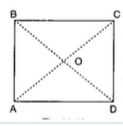
In quadrilateral ABCD,
AC and BD are diagonals which intersect at O.
In △AOB and △AOD
DO=OB (O is the midpoint)
AO=AO (Common side)
∠AOB=∠AOD (Right angle)
So, △AOB≅△AOD
So, AB=AD
Similarly, AB=BC=CD=AD
∴ABCD is a rhombus.
Hence Proved.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Prove that; If the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
ArhombusBtrapeziumCrectangleDkite - Question 2 - Select One
If the diagonals of a quadrilateral bisect each other at right angles, then this quadrilateral is
Aa rectangleBa rhombusCa kiteDnone of these
Prove that the if the diagonals of a quadrilateral bisect each other at right angles then it is a rhombus.
View SolutionShow that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
View SolutionIn figure, Show that if the diagonals of a quadrilateral are equal and bisect each other at right angle, then it is a square.
 View Solution
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
View SolutionIf the diagonals of a quadrilateral bisect each other at right angles, then this quadrilateral is a
View Solution

