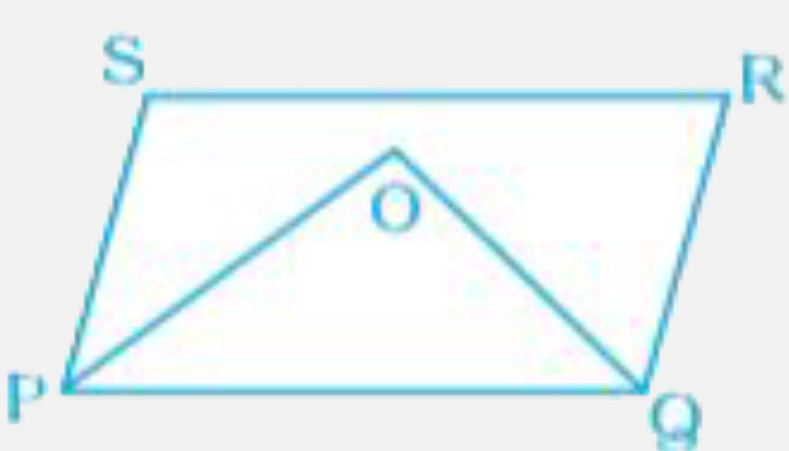
In Figure, PQRS is a parallelogram, PO and QO are, respectively, the angle bisectors of ∠P and ∠Q. Line LOM is drawn parallel to PQ. Prove that : PL=QM (ii) LO=OM
Given ∠1=∠2 and ∠4=∠5
PS||RQ
PL||MQ
PL||QM and LM||PQ
PLQM is a parallelogram
PL=QM
PQ||LM and QD is traversal
∠1=∠3
∠2=∠3
In∠OPL
∠2=∠3
DL=PL
PB||CM and OQ is tangent
∠4=∠6
∠5=∠6
In∠OQM
∠5=∠6
OM=QM
Put PL=QM
OL=OM.
Topper's Solved these Questions
Similar Questions
In Figure, PQRS is a parallelogram, PO and QO are, respectively, the angle bisectors of ∠P and ∠Q . Line LOM is drawn parallel to PQ . Prove that: PL=QM (ii) LO=OM
View SolutionPQRS is a square such that PR and SQ intersect at O. State the measure of ∠POQ
View SolutionIn a parallelogram PQRS, the bisectors of ∠P and ∠Q meet at O. Find ∠POQ.
 View Solution
View SolutionABCD is a parallelogram whose diagonals AC and BD intersect at O. A Line through O intersects AB at P and DC at Q. Prove that ar(△POA)=ar(△QOC).
View SolutionABCD is a parallelogram whose AC and BD intersect at O. A line through O intersects AB at P and DC at Q. Prove that ar ( POA)= ar ( QOC).
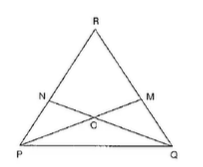
View SolutionIn Figure, ∠QPR= ∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN. Prove that OP=OQ, where O is the point of intersection of PM and QN
 View Solution
View SolutionIf the Boolean expression (p∧q)⊗(p⊕q) is a tautology ,then ⊗ and ⊕ are respectively given by :
View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.
 View Solution
View SolutionIn Fig. 4.90, if PSQR , prove that POS~ROQ . (FIGURE)
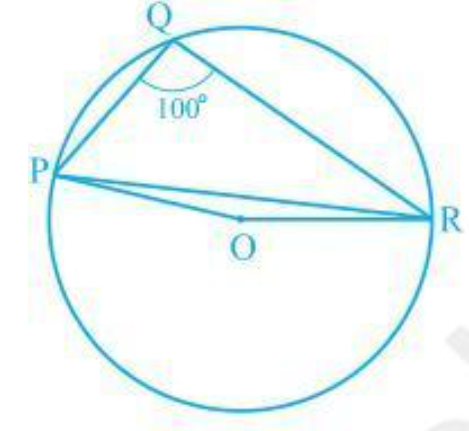
View SolutionIn Fig. 10.37, ∠PQR = 100∘, where P, Q and R are points on a circle with centre O. Find ∠OPR.
 View Solution
View Solution
