In figure,a right triangle ABC,circumscribes a circle of radius r.If AB and BC are of length 8 cm and 6 cm respectively, find the value of r.
To find the radius r of the circle that is inscribed in the right triangle ABC with sides AB=8 cm and BC=6 cm, we can follow these steps:
Step 1: Identify the lengths of the sides
Given:
- AB=8 cm
- BC=6 cm
Step 2: Use the Pythagorean theorem to find the length of the hypotenuse AC
The Pythagorean theorem states that in a right triangle:
AC2=AB2+BC2
Substituting the values:
AC2=82+62=64+36=100
Taking the square root:
AC=√100=10 cm
Step 3: Calculate the semi-perimeter s of triangle ABC
The semi-perimeter s is given by:
s=AB+BC+AC2
Substituting the values:
s=8+6+102=242=12 cm
Step 4: Use the formula for the radius r of the inscribed circle
The radius r of the inscribed circle can be calculated using the formula:
r=As
where A is the area of the triangle. The area A of a right triangle can be calculated as:
A=12×AB×BC=12×8×6=24 cm2
Step 5: Substitute the area and semi-perimeter into the radius formula
Now substituting the values into the formula for r:
r=2412=2 cm
Final Answer
Thus, the radius r of the inscribed circle is 2 cm.
---
Given:
- AB=8 cm
- BC=6 cm
The Pythagorean theorem states that in a right triangle:
AC2=AB2+BC2
Substituting the values:
AC2=82+62=64+36=100
Taking the square root:
AC=√100=10 cm
The semi-perimeter s is given by:
s=AB+BC+AC2
Substituting the values:
s=8+6+102=242=12 cm
The radius r of the inscribed circle can be calculated using the formula:
r=As
where A is the area of the triangle. The area A of a right triangle can be calculated as:
A=12×AB×BC=12×8×6=24 cm2
Now substituting the values into the formula for r:
r=2412=2 cm
Thus, the radius r of the inscribed circle is 2 cm.
Topper's Solved these Questions
Similar Questions
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BD and DC are of lengths 6 cm and 9 cm respectively. If the area of △ABC=54cm2, then find the lengths of sides AB and AC. ltBRgt
 View Solution
View SolutionIn Figure, triangle ABC is drawn to circumscribe a circle of radius 4cm such that the segments BDandDC are of lengths 8cm and 6cm respectively. Find the lengths of sides ABandAC, when area of ABC is 84cm2.
View SolutionIn the given figure , ABC is a right triangle, right angled at B. Medians AD and CE are of respective length 5 cm and 2√5cm . Find the length of AC.
 View Solution
View SolutionABC is an isosceles triangle inscribed in a circle of radius r. If AB=AC and h is the altitude form A to BC. If P is perimeter and A is the area of the triangle then find the value of limh→0AP3.
View SolutionIn the given figure, triangle ABC is circumscribing a circle. Find the length of BC, if AF=3 cm, FB=4 cm and AC= 9 cm
View SolutionIn figure ΔABC is circumscribing a circle. Find the length of BC
View SolutionA triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively. Find the sides AB and AC.
View SolutionIn the given figure △ABC is circumscribing a circle. Find the length of BC. Given AR=4cm, RB=3cm and AC=11cm.
 View Solution
View SolutionIn the given figure ΔABC is right angled at A. Semicircles are drawn on AB, BC and AC as diameters. It is given that AB=3 cm and AC=4cm then find the area of the shaded region
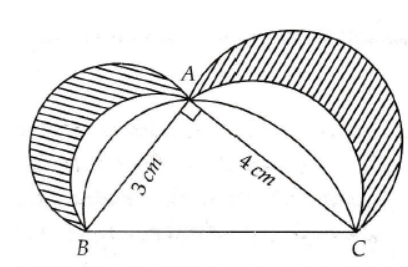 View Solution
View SolutionIn the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F respectively. If AB= 12 cm, BC= 8 cm and AC = 10 cm, find the lengths of AD, BE and CF.
View Solution

