In how many points the graph of meets the ?
The correct Answer is:One
To determine how many points the graph of the function f(x)=x3+2x2+3x+4 meets the x-axis, we need to find the roots of the equation f(x)=0. Here is a step-by-step solution:
Step 1: Set the function equal to zero
We start by setting the function equal to zero to find the roots:
x3+2x2+3x+4=0
Step 2: Differentiate the function
Next, we differentiate the function to analyze its behavior:
f′(x)=ddx(x3+2x2+3x+4)=3x2+4x+3
Step 3: Analyze the derivative
To determine the nature of the function, we need to analyze the derivative f′(x)=3x2+4x+3. We will find the discriminant of this quadratic function to see if it has any real roots:
D=b2−4ac=(4)2−4(3)(3)=16−36=−20
Step 4: Determine the nature of the roots
Since the discriminant D is negative, the quadratic f′(x) has no real roots. This implies that f′(x) does not change sign and is always positive because the coefficient of x2 (which is 3) is positive.
Step 5: Conclude about the function's behavior
Since f′(x)>0 for all x, the function f(x) is always increasing. An always increasing function can meet the x-axis at most once.
Step 6: Final conclusion
Thus, the graph of f(x)=x3+2x2+3x+4 meets the x-axis at exactly one point.
Summary
The graph of the function meets the x-axis at one point.
---
We start by setting the function equal to zero to find the roots:
x3+2x2+3x+4=0
Next, we differentiate the function to analyze its behavior:
f′(x)=ddx(x3+2x2+3x+4)=3x2+4x+3
To determine the nature of the function, we need to analyze the derivative f′(x)=3x2+4x+3. We will find the discriminant of this quadratic function to see if it has any real roots:
D=b2−4ac=(4)2−4(3)(3)=16−36=−20
Since the discriminant D is negative, the quadratic f′(x) has no real roots. This implies that f′(x) does not change sign and is always positive because the coefficient of x2 (which is 3) is positive.
Since f′(x)>0 for all x, the function f(x) is always increasing. An always increasing function can meet the x-axis at most once.
Thus, the graph of f(x)=x3+2x2+3x+4 meets the x-axis at exactly one point.
The graph of the function meets the x-axis at one point.
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - CONCEPT APPLICATION EXERCISE 2.7
9 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - CONCEPT APPLICATION EXERCISE 2.8
11 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - CONCEPT APPLICATION EXERCISE 2.5
4 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
294 Videos
Similar Questions
Knowledge Check
In how many different points does the graph of the function f(x)=x3−2x2+x−2 intersect the x-axis?
A0B1C2D3
In how many points graph of y=x3−3x2+5x−3 interest the x-axis?
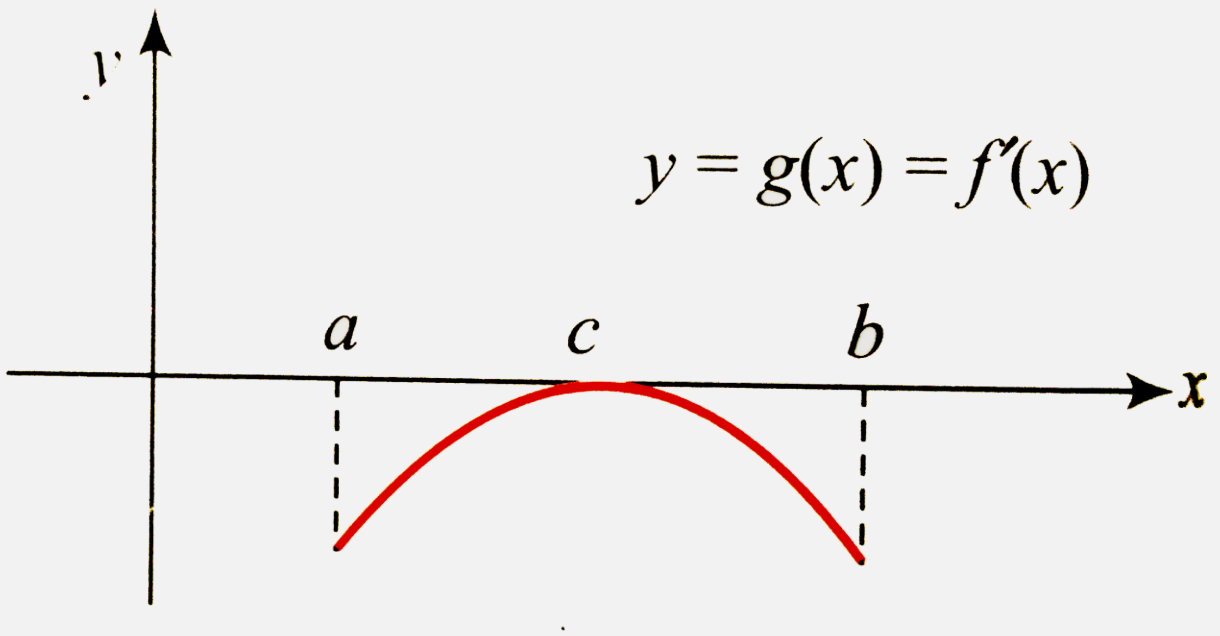
View SolutionFollowing is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
(d) Find the points of local maxima/minima ofy=f(x),a<xb.
(e) How many roots equation f''(x)=0 has?
View SolutionDraw and discuss the graph of f(x)=x2/3−x4/3
View SolutionHow many x-intercepts does f(x)=x2+3x+3 have?
View SolutionDraw the graph of f(x)=5x2(x−1)3.
View SolutionDraw the graph of f(x)=x3−xx2−1.
View SolutionDraw the graph of f(x)=(x−1)|(x−2)(x−3)|.
View Solution
